本文主要是介绍白话文讲HashMap,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在这片文章开始之前,我先抛出几个问题,读者可以先回忆或者思考一下,然后再继续往下看,看与读者之前的认识是否有冲突
1、HashMap底层是一种什么样的结构?
2、一个对象最后是如何确定到一个Hash桶的(如何确定数组中的一个位置)?
3、发生Hash冲突了如何解决?
4、为什么HashMap需要扩容?
5、为什么HashMap容量是2的幂次方
6、引入红黑树解决了什么样的问题?
7、什么时候扩容?是否不达到阈值就一定不扩容呢?
由于都是我自己的观点,所以希望读者能给我留言,说说读后感,交流一下,若有错误欢迎拍砖:
个人觉得HashMap这个东东可以挖掘出很多很多基础知识,当然这些东西都是我有意挖掘后整理的。
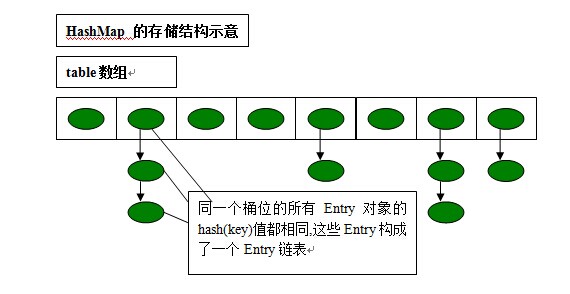
首先第一个问题:HashMap底层是一种什么样的结构?
答案大家肯定都知道:数组+链表,如下图所示:
为什么会是这样一种结构呢?
现在来说第二个问题,一个对象是如何定位到一个数组中的?
HashMap是一种key,value的键值对存储形式,当添加一个对象到HashMap中的时候,要进过以下过程:
1、获得该对象的hashcode
现在咱们假设有3个对象需要加入到HashMap中,这三个对象的hashcode分别是:
A:0100 0101 0110 1111 0101 0111 0110 0111
B:0100 0111 1111 0000 0010 1101 0011 1111
C: 0100 0111 1111 0000 0010 1101 0011 0001
2、经过一次扰乱函数(扰乱函数其实就是把对象的hashcode高16与低16位作与运算)重新获得32位的二进制数,这里博主主要想描述的不在于此,所以就假设经过扰乱函数之后,A、B、C三个对象的hashcode都不变 仍然是:
A:0100 0101 0110 1111 0101 0111 0110 0111
B:0100 0111 1111 0000 0010 1101 0011 1111
C: 0100 0111 1111 0000 0010 1101 0011 0001
3、用HashMap的size-1与第二步得到的hashcode作&(与运算),得到的数字是几,就把这个对象放在数组的第几个位置上,举例说明:
假设HashMap的size为8,则size二进制为:
0000 0000 0000 0000 0000 0000 0000 1000
那size-1之后的二进制数为:
0000 0000 0000 0000 0000 0000 0000 0111
这个时候size-1分别与A,B,C做与运算
例如与A作与运算:
0100 0101 0110 1111 0101 0111 0110 0111
0000 0000 0000 0000 0000 0000 0000 0111 &
————————————————————————
0000 0000 0000 0000 0000 0000 0000 0111
B、C与运算结果分别为:
0000 0000 0000 0000 0000 0000 0000 0111
0000 0000 0000 0000 0000 0000 0000 0001
上面说了,作完与运算之后数字就是放在数组中的位置,位运算之后结果转为10进制分别是 A:7,B:7,C:1
这个时候A和B由于计算结果相等(即发生了hash冲突)所以需要放在数组中的同一个位置,数组的一个位置只能放一个元素嘛,所以有了链表,所以HashMap才有了数组+链表的结构。
现在让我们再看看第4个问题:为什么HashMap需要扩容?
这个我觉得其实很有意思,大家学习容器的过程应该一般都是先学了ArrayList,LinkedList,然后学了HashSet,TreeSet,最后学了HashMap,不知道大家是不是这样,至少我是这样一个过程,导致了我很长一段时间内对HashMap的“扩容”产生了误解,我们知道ArrayList为什么需要扩容?就是因为ArrayList所维护的数组满了,放不下元素了,才扩容。
那HashMap扩容是不是也因为是放不下元素呢?
答案是:HashMap的扩容其实跟放不放得下完全没关系,大家想一下HashMap这种结构是不是永远不会满?如果HashMap中的数组满了,有新元素添加进来,也一定会插入到数组中的某条链表上,对吧?
那HashMap既然永远不会满,那为什么要扩容?扩容解决了什么样的问题呢?
先让我们想想HashMap这种数据结构设计的初衷:理想情况下,可以通过key的hash值在时间复杂度为O(1)拿到对应的Value对吧?那现在假设HashMap中的数组上每一个位置都有一条特别特别长的链表,那当我们通过key去定位到数组的某个位置了之后,是不是还需要遍历这个位置上的链表最终才能拿到那个元素?那时间复杂度就不是O(1)而近似为O(元素个数/数组长度)。
达不到理想状态怎么办呢?我们总得去解决这个问题吧?
于是有了两种解决方案:
1、在适当的时候,将数组扩容,你想想一下如果数组无限长是不是不同对象定位到数组中的同一个位置的概率就非常小了(数组无限长的时候只有在不同对象的Hashcode相等的时候才会出现)?
所以才有了什么负载因子,扩容机制这些东东,这些东东就解决一件事情,降低发生hash冲突的概率,降低发生hash冲突的概率就是跟我开始说的HashMap设计的初衷相合,即:发生hash冲突的次数越小,越接近理想情况,在时间复杂度为O(1)的情况下通过key去get到对应的value。
2、第二种解决方案比较有意思,即当链表长度达到8的时候,会执行树化函数,其实就是把链表转成一颗红黑树(个人觉得转红黑树是一种治标不治本的无奈之举),由于本文讨论的是HashMap,这里作者不需要专门去看红黑树,读者可以简单的理解红黑树是一颗近似平衡的二叉排序树,如果你也不知道什么是二叉排序树也不要紧,你就先记住在红黑树上找一个对象比在链表上找一个对象要快就行了,说白了链表转为红黑树就是为了提高HashMap中查找元素的速率。
文章一开始提到的问题,这里已经解决了一大半,既然说到了扩容,我先再好好说说扩容的时候发生了什么,之间原数组中的元素是放在新数组的同样索引的位置吗?
这个时候会重新定位数组中的每个对象的位置,让我们重新回顾一下A,B之前经过扰乱函数之后的值:
A:0100 0101 0110 1111 0101 0111 0110 0111
B:0100 0111 1111 0000 0010 1101 0011 1111
在数组长度为8的时候,A,B与(数组长度-1)作与运算之后都为7,大家应该都记得吧,A,B之前是在同一条链表上,扩容之后他们将重新定位到新的数组上,大家可以先根据前面知识,想一想A,B在新的数组上会不会发生hash冲突,即仍然定位到新数组上的同一位置呢?
答案是:不会。 why?
数组扩容后,新数组长度为16
二进制位:
0000 0000 0000 0000 0000 0000 0001 0000
新数组长度-1的二进制是:
0000 0000 0000 0000 0000 0000 0000 1111
然后用A、B的最终hash值与上述二进制作与运算,来看结果:
A:
0000 0000 0000 0000 0000 0000 0000 1111
0100 0101 0110 1111 0101 0111 0110 0111 &
————————————————————————
0000 0000 0000 0000 0000 0000 0000 0111
-
B:
0000 0000 0000 0000 0000 0000 0000 1111
0100 0111 1111 0000 0010 1101 0011 1111
————————————————————————
0000 0000 0000 0000 0000 0000 0000 1111
发现没有?A是0111 而B是1111,A是7,B是15,换句话说A定位在新数组的第7位置上,B定位在新数组的第15位置上,分开了,很神奇有木有?
结论来了:在扩容的时候,原数组的链表会分成两条链表,一条链表在新数组的原索引位置,一条链表在新数组的新索引位置,而且这两条链表在概率上是近乎相等的,可能有点绕,读者就看上面A、B的情况,A之前在旧数组的第7个位置,在扩容后,A仍在在新数组的第7位,而B之前在旧数组的第7位,扩容后在新数组的第15位。有点扯,扩容就可以把链表变短也~扩容一次链表几乎变短一半,很神奇有没有~~
还没写完,这是我来百度的第二天,现在时间是晚上10:08分,周围还很热闹,我没事干写了这篇文章,有点点累准备回家睡觉了~~ 之后接着更新
这篇关于白话文讲HashMap的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!