本文主要是介绍统计学习--HMM,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
隐马尔可夫模型的定义:
HMM 是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。(p171)
隐藏的马尔可夫链随机生成的状态的序列,称为状态序列。
每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列。
序列的每一个位置又可以看作是一个时刻 t。
隐马尔可夫模型由初始概率分布( π \pi π)、状态转移概率分布(A)以及观测概率分布(B)确定。
-
一个模型:HMM三要素:
A = [ a i j ] N ∗ N A=\left[ a_{ij} \right]_{N*N} A=[aij]N∗N,其中, a i j = P ( i t + 1 = q j ∣ i t = q i ) , i = 1 , 2 , . . . , N a_{ij}= P(i_{t+1}=q_j | i_t = q_i),i=1,2,...,N aij=P(it+1=qj∣it=qi),i=1,2,...,N
B = [ b j ( k ) ] N ∗ M B=\left[ b_j(k) \right]_{N*M} B=[bj(k)]N∗M,其中, b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , . . . , M ; j = 1 , 2 , . . . , N b_j(k) = P(o_t = v_k | i_t = q_j),k=1,2,...,M;j=1,2,...,N bj(k)=P(ot=vk∣it=qj),k=1,2,...,M;j=1,2,...,N
π = ( π i ) \pi = (\pi_i) π=(πi),其中, π i = P ( i 1 = q i ) , i = 1 , 2 , . . . , N \pi_i = P(i_1=q_i),i=1,2,...,N πi=P(i1=qi),i=1,2,...,N -
HMM两个基本假设
齐次马尔可夫性假设,即t 时刻状态只依赖于t-1时刻,与其他状态或观测无关。
观测独立性假设,即任意时刻的观测只依赖于该时刻的状态。
例子》 盒子和球 -
HMM的3个基本问题

(1)evalution: 概率计算问题
直接计算法、前向算法、后向算法
(2)learning:学习问题
监督学习算法:根据观测和状态序列计算频数,进而求得频率,最终求得到A、B、 π \pi π
非监督学习算法:(Baum-Welch算法,即EM)目标也是学习HMM模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)的参数
(3)decoding:预测问题,也叫解码问题。
近似算法:在每个时刻t 选择该时刻最有可能出现的状态 i t ∗ i_t^{*} it∗,从而得到一个状态序列 I ∗ = ( i 1 ∗ , i 2 ∗ , … , i T ∗ ) I^{*} = (i_1^{*},i_2^{*},\dots,i_T^{*}) I∗=(i1∗,i2∗,…,iT∗),将它作为预测的结果。
维特比算法:
动态规划解隐马尔可夫模型预测问题,即用动态规划求概率最大路径(最优路径),这时一条路径对应一个状态序列。
初始化
递归:
终止:最大概率
回溯:上一个节点
总结————————————————
Dynamic Model
—HMM( mixture + time )
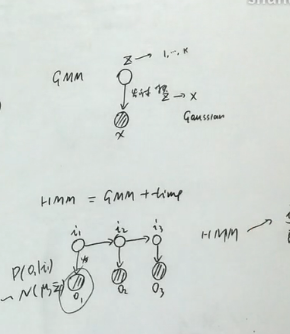
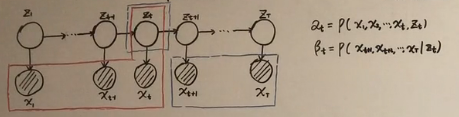

参考:
白板推导

主要涉及5个算法:
Baum-Welch/ EM
Viterbi algorithm
Forward Algorithm
Backward Algorithm
Forward-Backward Algorithm
这篇关于统计学习--HMM的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





