本文主要是介绍6月软考新通知:24下集成大概率是中级蕞简单的一门,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2024下半年软考6月新通知:
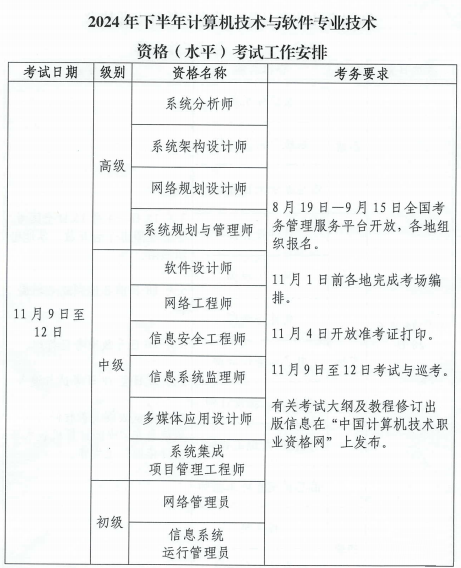
一、24下软考考试时间安排:
24下半年软考报名时间:8月19日-9月15日
24下半年软考考试时间:11月9-12日
24下半年软考成绩查询:12月中(预计)

二、考情分析
24上软考已于5.26日结束,24下新一轮软考又要开启了!今天给大家总结了要过24下软考会用到的一些事半功倍的工具,以及备考方法分享给大家!
有打算备考24下软考的可以开始准备喽!今年软考大改革很多科目都变成了1年1考,宝子务必抓住机会!如果你上半年考了高级信息系统没有特别大的把握、下半年考系统集成就很合适,因为考试内容有70%的重合度,上岸几乎稳了。

三、软考证书有什么用?
1. 以考代评:获得对应软考证书即获得对应职称,无需再进行评测(具体看单位和地区规定)。
2. 积分落户:可用于积分落户,加相应的分,软考高级职业资格都几乎可以直接落户。
3. 企业招标:企业在申请项目需要达到一定的资质。
4. 入选当地评审专家库和评标专家库:若具备高级职称且工作年限满足要求即可。
5. 个人发展自身能力的提升:若就职于国企,事业单位,公务员相关岗位,那么软考的中高级资格,对职业发展和提升至关重要!
四、备考建议
注意:如果你备考中级软考系统集成这个科目,根据章节分值,正确的备考顺序应该是:
先4-19章(40分),再1-3(26分)章,蕞后20-23章(6-7分)

备考时间规划:
(如果从6.1开始)
6.1-8月
①按照以上列举顺序跟着软考基础网课过1遍教材知识点,一些重点可以补充在三色高频考点笔记上
②听完课,先别急着做题,对着三色笔记和教材,梳理一遍知识框架
③然后找个题库app刷章节题并及时订正消化
④一轮对背诵要求不高,多读,理解更重要
9月-10月
①主要看《系统集成》重点章节(第1、3、4-19章)以及计算题和案例分析题专项课,有时间用默写本二次巩固一下
②此阶段要多刷题,会应用。先二刷章节母题,再刷毕考100题、蕞后再刷中级软考系统集成近5年真题,20年以后的真题重点刷+背
③【案例分析题万金油80条】5-10条/天,并能在案例题中熟练应用,三色考点笔记勤快点背
11月初-考前
①重点掌握10大管理+47个子过程,反复看错题还有一些易错易混知识点
②三刷章节题(只刷错题部分),二刷软考中级近5年真题,总结好答题技巧
③考前进行2-3次模拟(23年开始改机考)感受真实考试情境
④狂背万金油、公式、记忆口诀和三色考点笔记(红色部分)
写在最后
如果你正在备战软考或计划备战软考,需要资料的可以私我或留言,纸质资料已经给别人了,还剩很多电子资料,有课程视频、课件、资料、考试要点、论文写作、论文集等,扫一扫加【2024软考备考大部队】:

这篇关于6月软考新通知:24下集成大概率是中级蕞简单的一门的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




