本文主要是介绍【代码随想录】【算法训练营】【第27天】 [39]组合总和 [40] 组合总和II [131]分割回文串,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
思路及算法思维,指路 代码随想录。
题目来自 LeetCode。
day26, 休息的周末~
day 27,周一,库存没了,哭死~
题目详情
[39] 组合总和
题目描述
39 组合总和

解题思路
前提:组合的子集问题,统一元素可以重复选取
思路:回溯 + 剪枝。
重点:剪枝的前提是数组已排序。
代码实现
C语言
回溯 + 未排序剪枝
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, int ***ans, int* returnSize, int** returnColumnSizes)
{// 退出条件if (0 == target){*ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));(*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));for (int i = 0; i < numsSize; i++){(*ans)[*returnSize][i] = nums[i];}*returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));(*returnColumnSizes)[*returnSize] = numsSize;(*returnSize)++;return ;}for (int j = index; j < candidatesSize; j++){if (target < candidates[j]){continue ;}// 递归nums[numsSize] = candidates[j];numsSize++;backtracing(candidates, candidatesSize, target - candidates[j], j, nums, numsSize, ans, returnSize, returnColumnSizes);// 回溯numsSize--;nums[numsSize] = 0;}return ;
}int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {// 判空if (candidatesSize == 0){return NULL;}// 输出int **ans = NULL;int nums[41];int index = 0;*returnSize = 0;printf("%d\n", target);backtracing(candidates, candidatesSize, target, 0, nums, 0, &ans, returnSize, returnColumnSizes);if (*returnSize == 0){return NULL;}return ans;
}
回溯 + 排序 + 剪枝
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/int cmp(const void *p1, const void *p2)
{return *(int *)p1 > *(int *)p2;
}void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, int ***ans, int* returnSize, int** returnColumnSizes)
{// 退出条件if (0 == target){*ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));(*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));for (int i = 0; i < numsSize; i++){(*ans)[*returnSize][i] = nums[i];}*returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));(*returnColumnSizes)[*returnSize] = numsSize;(*returnSize)++;return ;}// 剪枝for (int j = index; (j < candidatesSize) && (target >= candidates[j]); j++){// 递归nums[numsSize] = candidates[j];numsSize++;backtracing(candidates, candidatesSize, target - candidates[j], j, nums, numsSize, ans, returnSize, returnColumnSizes);// 回溯numsSize--;nums[numsSize] = 0;}return ;
}int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {// 判空if (candidatesSize == 0){return NULL;}// 排序qsort(candidates, candidatesSize, sizeof(int), cmp);// 输出int **ans = NULL;int nums[41];int index = 0;*returnSize = 0;backtracing(candidates, candidatesSize, target, 0, nums, 0, &ans, returnSize, returnColumnSizes);if (*returnSize == 0){return NULL;}return ans;
}
[40] 组合总和II
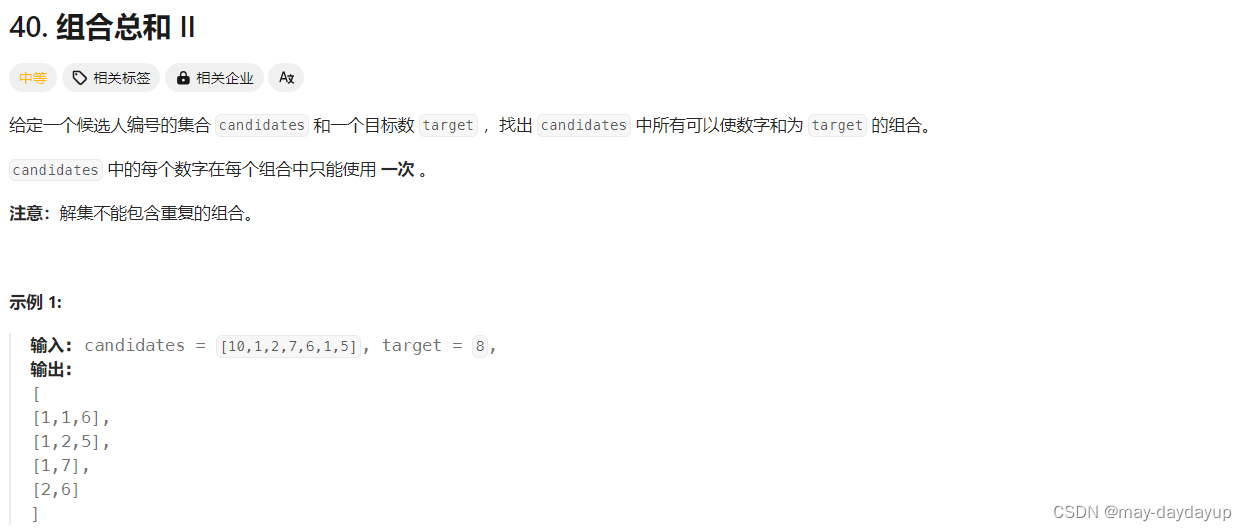
题目描述
40 组合总和II
解题思路
前提:组合的子集问题,同一元素只能使用一次,但是结果不包含重复组合
思路:回溯 + 剪枝
重点:结果子集中排除重复组合,需要树形结构中,同一树层的相同的元素值不可重复选取,使用used数组实现去重。
代码实现
C语言
利用used数组 false,同一树层 去重
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/int cmp(const void *p1, const void *p2)
{return *(int *)p1 > *(int *)p2;
}void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, bool *used, int ***ans, int* returnSize, int** returnColumnSizes)
{// 退出条件if (0 == target){*ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));(*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));for (int i = 0; i < numsSize; i++){(*ans)[*returnSize][i] = nums[i];}*returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));(*returnColumnSizes)[*returnSize] = numsSize;(*returnSize)++;return ;}for (int j = index; (j < candidatesSize) && (target >= candidates[j]); j++){// 去重if ((j > 0) && (candidates[j] == candidates[j - 1]) && (used[j - 1] == false)){continue;}// 递归nums[numsSize] = candidates[j];used[j] = true;numsSize++;backtracing(candidates, candidatesSize, target - candidates[j], j + 1, nums, numsSize, used, ans, returnSize, returnColumnSizes);// 回溯numsSize--;used[j] = false;nums[numsSize] = 0;}return ;
}int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {// 判空if (candidatesSize == 0){return NULL;}// 排序qsort(candidates, candidatesSize, sizeof(int), cmp);// 输出int **ans = NULL;int nums[100] = {0};bool used[100] = {false};int index = 0;*returnSize = 0;backtracing(candidates, candidatesSize, target, 0, nums, 0, used, &ans, returnSize, returnColumnSizes);if (*returnSize == 0){return NULL;}return ans;
}
[131] 分割回文串
题目描述
131 分割回文串

解题思路
前提:分割问题
思路:。
重点:。
代码实现
C语言
// 待补充
今日收获
- 组合子集问题:去重,同一树层去重 vs 同一树杈去重
- 切割问题。
这篇关于【代码随想录】【算法训练营】【第27天】 [39]组合总和 [40] 组合总和II [131]分割回文串的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






