本文主要是介绍计算机组成原理 第六章 计算机的运算方法 Part1，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
无符号数和有符号数
1.无符号数
寄存器位数反映无符号数的表示范围：
8位——0~255
16位——0~65535
2.有符号数
原码表示法
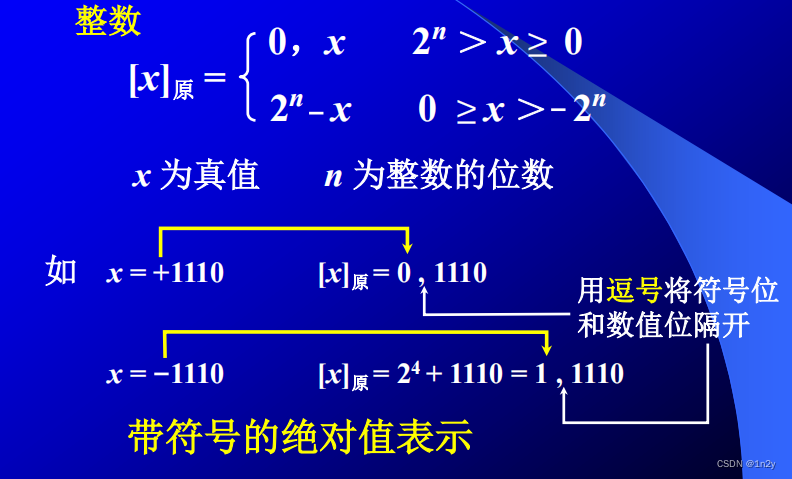
- 原码简单直观
- 举例
原码表示法的局限性
原码的特点：简单、直观
但是用原码做加减法时，应分但是用原码做加减法时，应分情况讨论： 情况讨论：
可否简化？ 符号位与数值位一起参加运算；只做加法，不做减法
补码表示法
概念
- 补码的提出：解决原码的加减符号不同意问题（用加法代替减法）
- 时钟：6点 -3 可用 + 9 代替-都变成3点，称 + 9 是 3 以 12 为模的补数（mod 12）
- 结论：
一个负数加上 “模” 即得该负数的补数
一个正数和一个负数互为补数时它们绝对值之和即为模数
特征
不同于原码，0 在补码中只有 00…0 一种表示形式
正数的补码与其原码相同
负数的补码（m 位）与其相反数的补码相加，结果 等于模（
），因此:
负数的补码可由其相反数的补码 按位取反，末位加 1
正数的补码也可由其相反数的补码 按位取反，末位加 1 求得
注意：
的补码 100…0 是一个特例，不适用上述
规律
求得
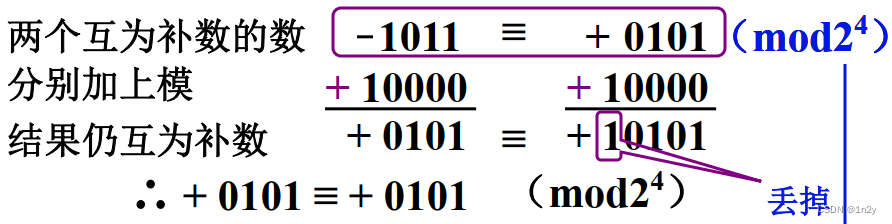
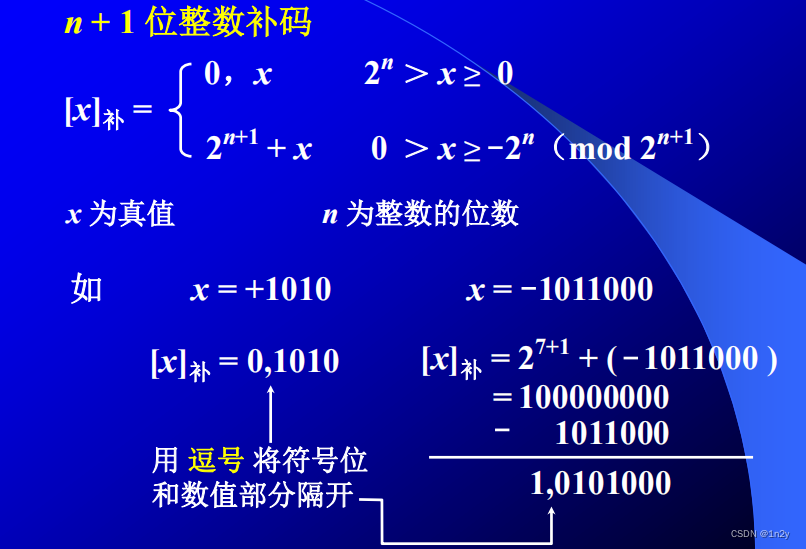
补码定义
当真值为负时，补码 可用 原码除符号位外每位取反，末位加 1 求得
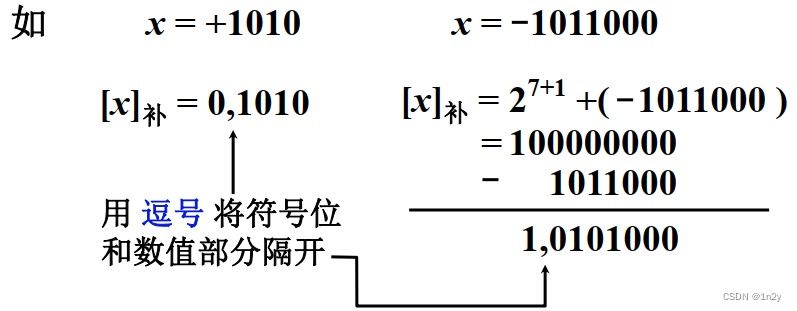
举例
小结
最高位为符号位，手写时整数用“, ” 小数用“.”将数值部分和符号位分隔
对于正数，原码 = 补码
对于负数 ，符号位为 1，其数值部分：
原码除符号位外每位取反末位加 1 ——》 补码
补码除符号位外每位取反末位加1 ——》 原码
注意 100…0 这个特例
课后例题6.2
反码表示法
除符号位每位取反
比较
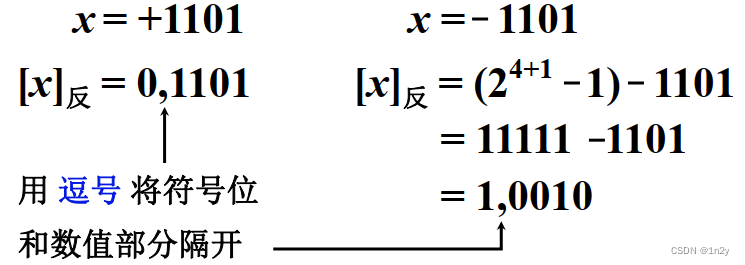
移码表示法
移码和补码的比较:补码与移码只差一个符号位
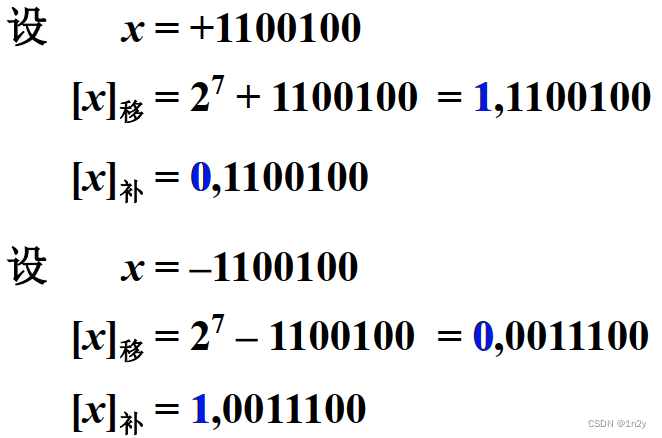
真值、补码和移码的对照
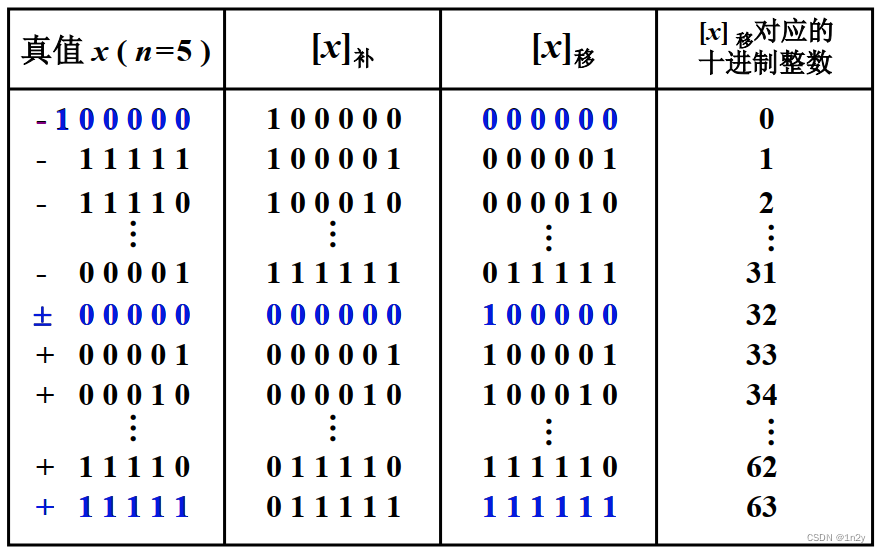
特点
最小真值的移码为全 0
用移码表示浮点数的阶码能方便地判断浮点数的阶码大小
这篇关于计算机组成原理 第六章 计算机的运算方法 Part1的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
