【刷题】初探递归算法 —— 消除恐惧

本文主要是介绍【刷题】初探递归算法 —— 消除恐惧，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

1 递归算法

在解决一个规模为 n 的问题时，如果满足以下条件，我们可以使用递归来解决：

1. 问题可以被划分为规模更小的子问题，并且这些子问题具有与原问题相同的解决方法。
2. 当我们知道规模更小的子问题（规模为 n-1）的解时，我们可以直接计算出规模为 n 的问题的解。
3. 存在一种简单情况，或者说当问题的规模足够小时，我们可以直接求解问题。这里一般成为函数出口（非常重要）

一般的递归求解过程如下：

1. 验证是否满足简单情况：
   简单情况是指问题规模非常小，通常可以直接得到答案的情况。我们需要首先检查当前问题是否满足这种情况。

2. 假设较小规模的问题已经解决，解决当前问题：
   在递归中，我们假设已经解决了规模较小的子问题，然后基于这些子问题的解来构建当前问题的解。这种假设称为“递归假设”。

总结来说，递归代码的编写如同使用一个“黑盒”一样，我们需要相信递归调用会正确解决子问题，而我们只需要关注处理当前的问题。

下面我们通过一个具体实例来展示如何在实践中解决问题：

假设我们要计算斐波那契数列中的第 n 项。斐波那契数列的定义如下：
$\text{F}(0)=0$
$\text{F}(1)=1$
对于 $n\ge 2$，$\text{F}(n)=\text{F}(n-1)+\text{F}(n-2)$

在这个问题中：
简单情况是 $\text{F}(0)$ 和 $\text{F}(1)$，我们可以直接得到答案。
对于其他情况，我们假设 $\text{F}(n-1)$ 和 $\text{F}(n-2)$ 已经计算出来，然后通过 $\text{F}(n)=\text{F}(n-1)+\text{F}(n-2)$ 计算出 $\text{F}(n)$。

这种递归解决问题的方法非常强大，但也需要注意避免过度递归带来的性能问题，比如栈溢出或时间复杂度过高等。

接下来我们一起来解决问题吧！！！

2 Leetcode 面试题 08.06. 汉诺塔问题

上连接： 面试题 08.06. 汉诺塔问题

题目描述

汉诺塔是个非常有意思的问题,其典故更是神乎其神：

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

题目给我们了xyz三个容器模拟柱子，我们需要模拟实现移动的过程，将X容器中的盘子移动到Z中。

算法思路

乍一看我们想不到什么思路，所以我们先来画图分析一波：

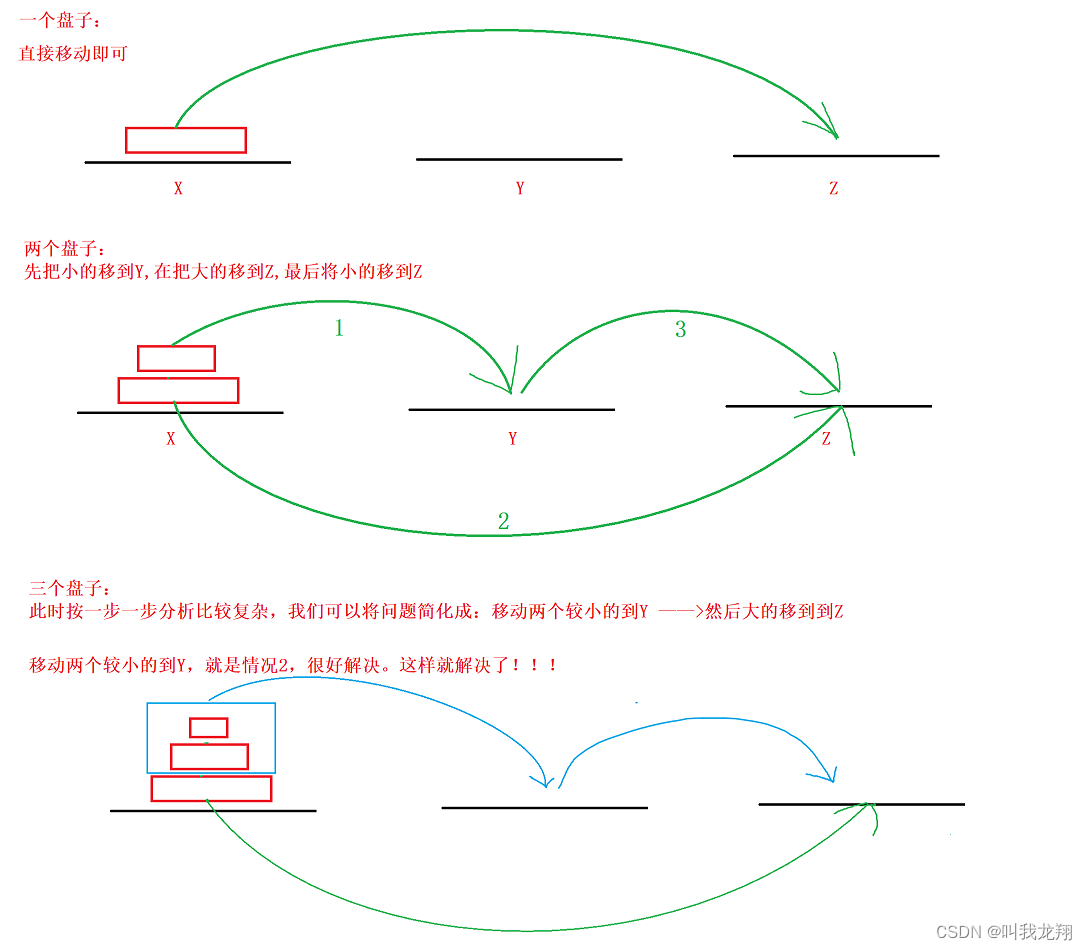
通过这三种情况我们就能分析出来，这道题可以被拆分成许多子问题来解决：

如果想要移动n个盘子

1. 先把 n - 1 个盘子移到中转柱子上，再把第n个移到目标柱子上。
2. 接下来处理 这n - 1 个盘子，把 n - 2 个小盘子移到中转柱子上，第 n - 1个移动到目标柱子上。
3. 重复 1 2 直到解决问题…

注意

    // x 为当前柱子 y 为中转柱子 z 为目标柱子 //我们只需要注意解决当前的问题，子问题交给黑盒处理void dfs(vector<int>& x, vector<int>& y, vector<int>& z , int n ){   //递归出口if(n == 1){int tmp = x.back();z.push_back(tmp);x.pop_back();return ;}//将 n 个盘子从 X 转移到 Z //则先把 n-1个盘子移到 Ydfs(x , z , y , n - 1);//然后此时X只有一个最大的盘子， 移到Zint tmp = x.back();z.push_back(tmp);x.pop_back();//现在 Y 上有 n-1 个盘子继续进行移动到Z上dfs(y , x , z , n - 1);return ;}void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {int n = A.size();dfs(A , B , C , n);return ;}

提交：过啦！！！

3 Leetcode 21. 合并两个有序链表

上连接！家人们：21. 合并两个有序链表

题目描述

很好理解的题目！

算法思路

相信大家看到这个题，肯定有迭代循环思路，但是今天我们通过递归来解决问题：

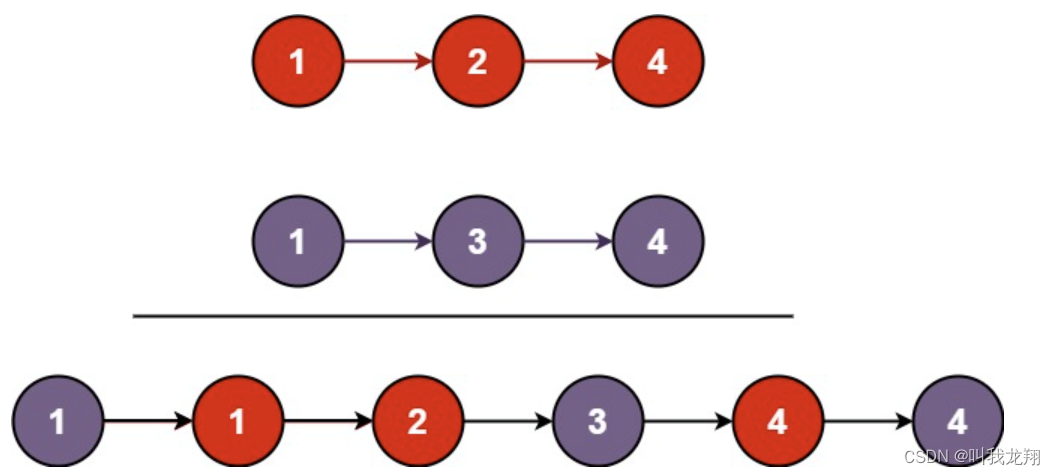
我们首先分析一下：

• 当前问题：当我们处理当前情况时，我们需要把后续处理交给黑盒，我们需要的是将较小的节点插入到新链表中！
• 子问题：处理除去以被处理的“较小的节点”之外的链表节点，使其合并。
• 函数出口：当我们处理到两个链表都为空时直接返回，或者一方为空直接返回另一链表即可！

    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {//处理为空的情况if(l1 == nullptr) return l2;if(l2 == nullptr) return l1;//都不为空，选择较小值进行插入！！！if(l1->val < l2->val){//l1 小 就把它的next交给黑盒处理l1->next = mergeTwoLists(l1->next , l2);//然后将它返回（这样黑盒才可以获取当前节点的next节点）return l1;}else{//l2 小 就把它的next交给黑盒处理l2->next = mergeTwoLists(l1 , l2->next);return l2;}}

提交：过啦！！！

4 Leetcode 206. 反转链表

上链接： 206. 反转链表 ！

题目描述

同样很好理解，接下来我们来使用递归解决问题

算法思路

首先这道题需要注意的一点是：我们要先找到新链表的头（即当前链表的尾节点）黑盒的返回值设置为新链表的头，然后再来进行反转。就类似二叉树的后序遍历。我们不能从链表的头开始反转到尾（先序遍历）。因为这样就无法获取新链表的头结点了

从宏观来看：我们只需要处当前问题：

1. 子问题： 后续节点的反转！黑盒会返回我们的头结点。我们的黑盒一定可以帮助我们解决后序的节点的反转。
2. 当前问题：把当前节点插入到以被反转的链表后，把当前节点的next设置为空即可！
3. 函数出口：当走到链表结尾即为出口！

ListNode* reverseList(ListNode* head) {//寻找新的头结点if( head == nullptr || head->next == nullptr ) return head;ListNode* newhead = reverseList(head->next);//进行倒置head->next->next = head;//next设置为空head->next = nullptr;//返回新链表的头return newhead;}

提交：过啦！！！

5 Leetcode 24. 两两交换链表中的节点

跟上节奏：24. 两两交换链表中的节点 ！！！

题目描述：

题目也很好理解奥

算法思路

我们依旧是使用递归来解决：

1. 当前问题：置换两个节点，并指向后续以及置换完成的链表。
2. 子问题：后序节点的置换
3. 函数出口：为空或只有一个节点之间返回即可。

    ListNode* swapPairs(ListNode* head) {//利用递归解决问题//一次要处理两个节点if(head == nullptr) return nullptr;if(head->next == nullptr) return head;//继续处理 --- 相信 swapPairs(tmp) 这个会处理好剩余部分ListNode* tmp = swapPairs(head->next->next);//进行处理//记录下 1 2 节点的后面的2节点，它是置换后的头节点。ListNode* ret = head->next;//置换head->next->next = head;head->next = tmp;return ret;}

提交：过啦！！！

6 Leetcode 50. Pow(x, n)

最后一题：50. Pow(x, n) ！！！

题目描述

这道题需要我们使用幂函数，当然不是一般的循环相乘（必然超时），我们要实现快速幂！

算法思路

快速幂的思想很简单：假如我们需要 2¹⁰ ,我们就求2⁵ ，求 2⁵ 就求 2² * 2² * 2 …以此类推直到次数为 0 就返回 1

需要注意的是负数的处理，求负次幂，我们可以先求正的然后在取倒数。
还有边界的处理，题目所给的最小值 - 2³¹ 取正后为 2³¹，超出int的范围，所以需要转换为long long

    double myPow(double x, long long n) {if(n == 0) return 1;if( n < 0 ) {long long t = (long long)(-n);double tmp = myPow( x , t / 2);return t % 2 == 0 ? 1 / (tmp * tmp) : 1 / (tmp * tmp * x);}else{double tmp = myPow( x ,  n / 2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}}

提交过啦！！！

7 总结

我们进行递归算法，只需要处理好当前问题，其余相信我们的黑盒可以解决。注意：

1. 函数出口的设置，这个是关键！！！
2. 返回值的设置要合适，看题分析！！！

Thanks♪(･ω･)ﾉ谢谢阅读！！！

下一篇文章见！！！

这篇关于【刷题】初探递归算法 —— 消除恐惧的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---