本文主要是介绍快速排序(排序中篇),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.快速排序的概念及实现
2.快速排序的时间复杂度
3.优化快速排序
4.关于快速排序的细节
5.总代码
1.快速排序的概念及实现
1.1快速排序的概念
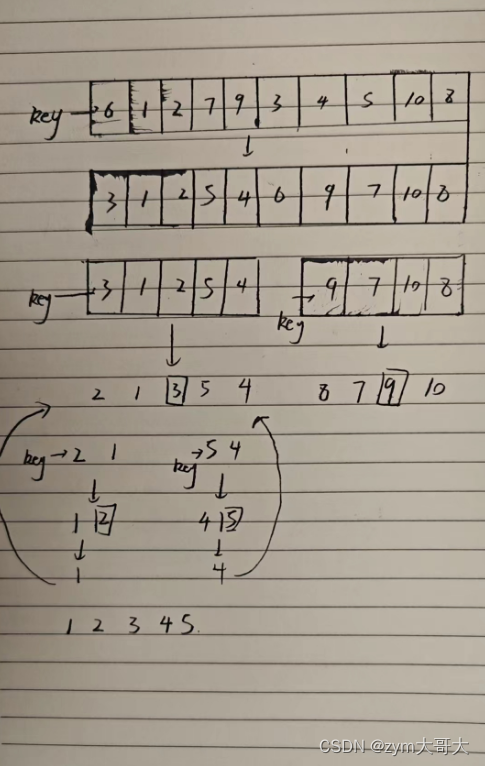
快速排序的单趟是选一个基准值,然后遍历数组的内容把比基准值大的放右边,比基准值小的放在左边,下面的动图可以简单了解是这么排序的。
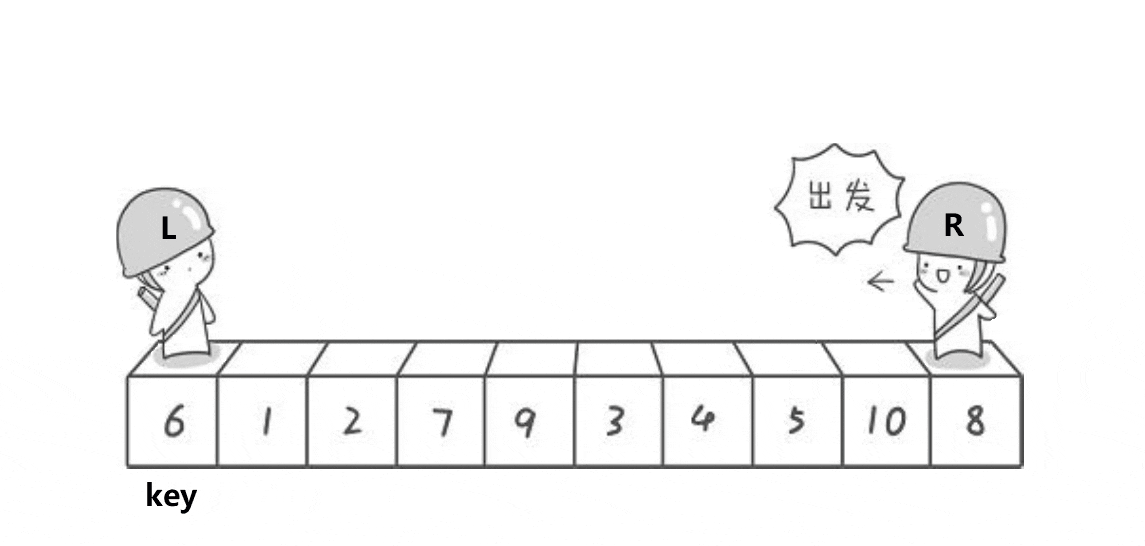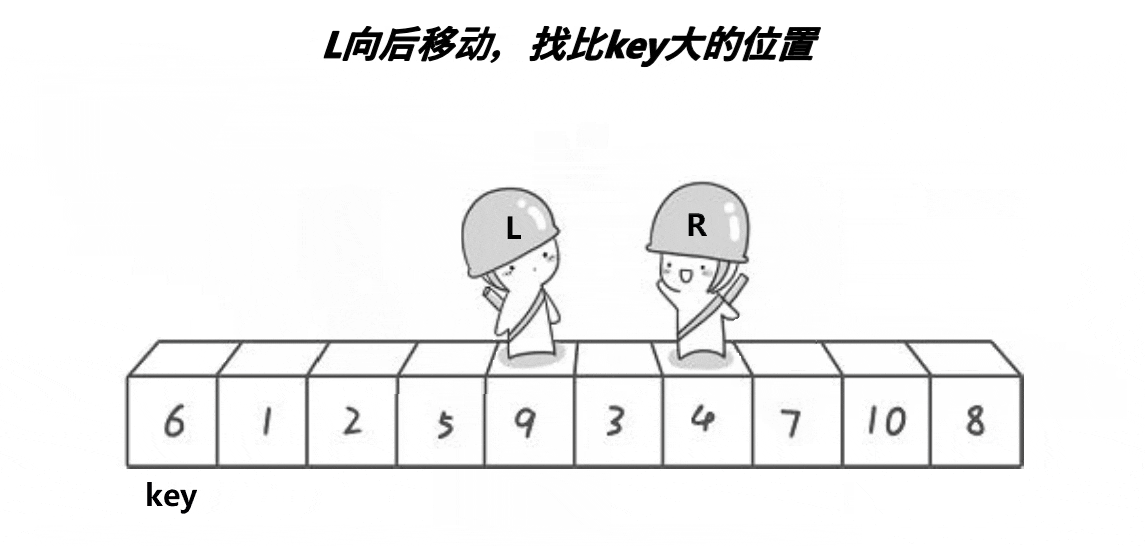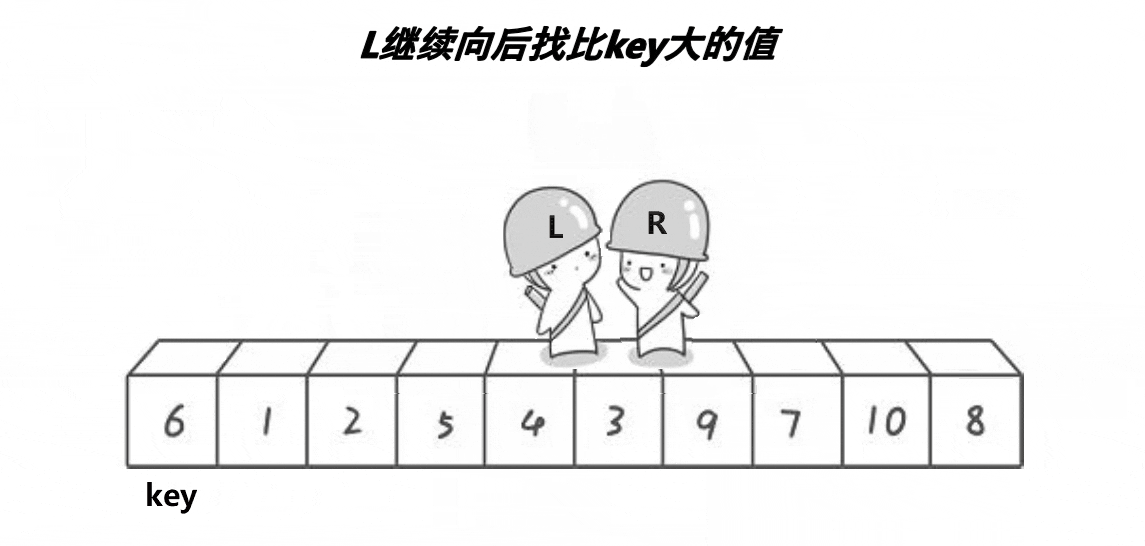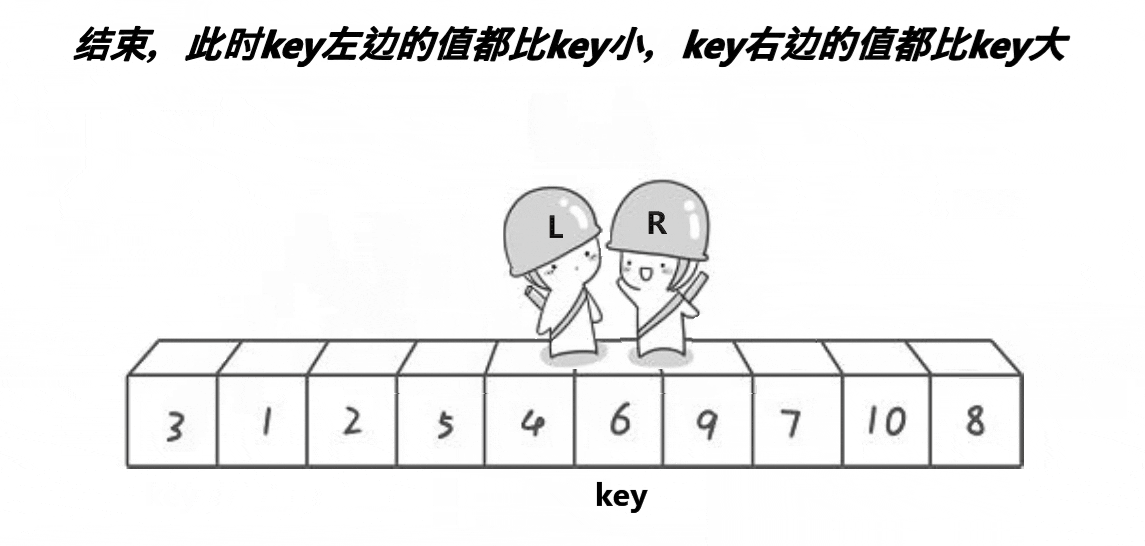
选第一个6作为基准,然后让俩个变量作为下标值去遍历数组,L要选出一个比key(6)要大的值然后停下,R要找到一个比key要小的值然后停下,最后把L和R停下的位置对应的值进行交换,交换完后有继续走,直到L与R相遇,最后把碰面的地方对应的值与key交换,完成一次单趟的快排 ,这样key的左边都是比key小的值,而右边都是比key大的值,与之前比较变得相对有序。
走完单趟后,后面就会以key的左右边重读第一次操作,就是把数组以key为分界线分为俩个数组(逻辑上),再选出一个基准值,使得基准值的俩边要么比key大要么比key小,这样就会想到递归,一直分到后面就会出现只有一个值的数组,或者不存在的(后面会提到),递归完后的数组就是排好序的了。
1.2快速排序的实现
代码:
#include<stdio.h>
void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void QuickSort(int* a,int left, int right)
{if (left >= right)return;int begin = left;int end =right;int keyi = left;while (begin< end){while (begin < end && a[keyi] <= a[end]){end--;}while (begin < end && a[keyi] >= a[begin]){begin++;}swap(&a[begin], &a[end]);}swap(&a[keyi], &a[begin]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
int main()
{int arr[] = { 11,7,5,9,6,1,4,3,8,8,8,101 };int size = sizeof(arr) / sizeof(arr[0]);QuickSort(arr,0,size-1);for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
}代码分析:
创建begin和end来作为L和R去遍历数组,while循环执行的条件是begin<end(这个是begin和end相遇的情况)与基准值比end下标对应的值小,满足就end--(就是往前走),begin就去找比基准值大的值才会执行条件,否则就begin++(往后走),但俩个while都执行完,就说明L与R都停下来了,就可以进行交换,交换完后while循环结束,出循环后就交换基准值与相遇地方对应的值,然后递归去keyi两边的数组排序,则keyi+-1就是它们的新边界,最前面的if判断是否存在可以排序,因为一个和不存在是排不了的。
下图是不存在的情况:

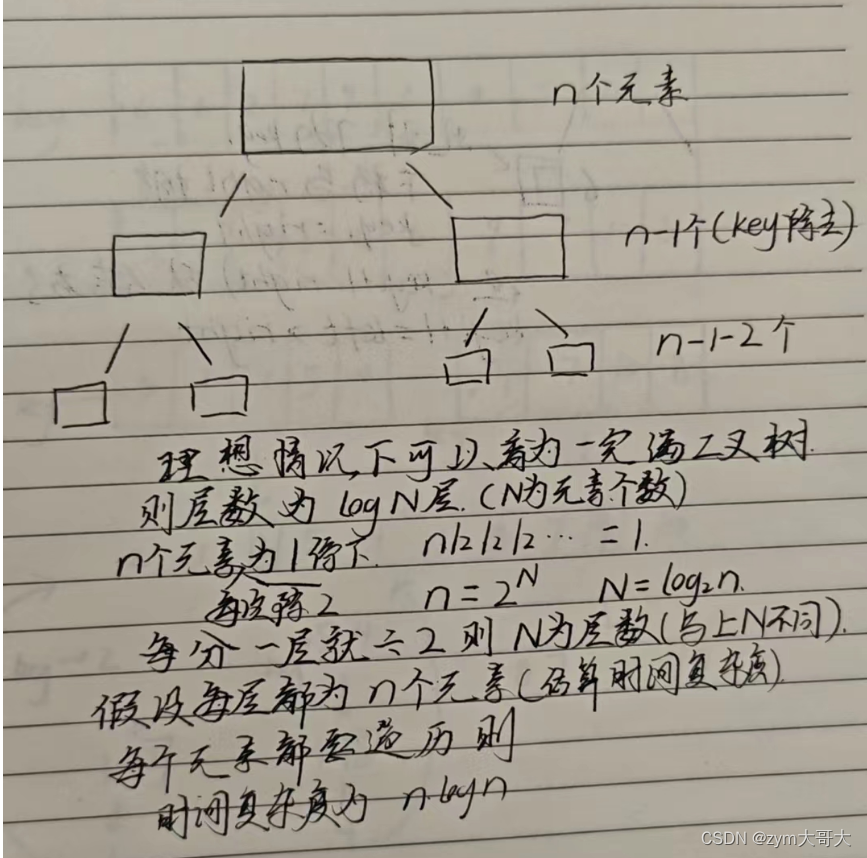
2.快速排序的时间复杂度
本文只是简单计算快速排序的时间复杂度。
3.优化快速排序
3.1三数取中
快速排序遇到有序的数组就会出现问题,时间复杂度会变为O(N^2).

基准值到最后还是原来的位置,则递归时,每次只会去掉第一个元素,不会像对半分那种,这样每层大约n个,层数也为n个,时间复杂度就为O(N^2),速度会慢很多,所以基准值不应该每次取第一个,可以用随机函数来获取一个拟随机数作为key值,但是也是有可能是最小或者最大(在排升序或者降序会慢),所以用三数取中的方法来定key,但是得到key值还是要和第一个值交换一下,保证上面的代码逻辑不变,假如下标为3的值适合作key就把它和第一个交换。

在有序的情况下插入排序都比快速排序快很多,而且在数据量大的时候会发生栈溢出,是一直递归开辟空间而导致的。
三数取中就是在数组中找到一个值不是最大也不是最小。
三数取中代码实现:
int GetMidi(int*a,int left, int right)
{int midi = (left + right) / 2;if (a[midi] < a[right]){if (a[midi] > a[left]){return midi;}else{if (a[left] > a[right])return right;elsereturn left;}}else//a[midi]>a[right]{if (a[midi] > a[left]){if (a[right] > a[left])return right;elsereturn left;}elsereturn midi;}
}代码分析:
就是在数组的最左右边及它们和一半值共三个数,然后比较三个值找到处于中间值的下标,这个值一定不是最小或者最大,比较数组的值返回下标,这样尽管处理有序数组也不会有栈溢出的风险,也能提高运行速率。
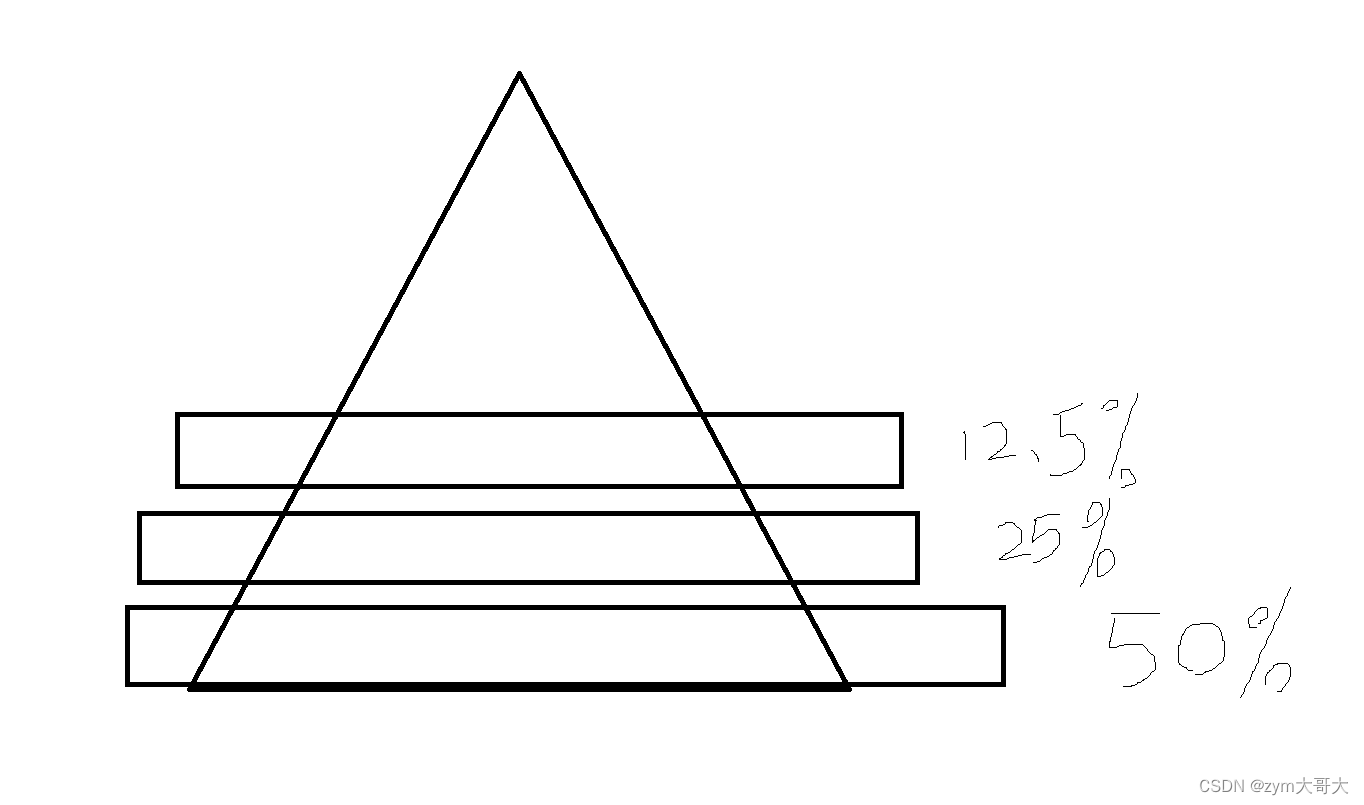
3.2小区间优化
因为在二叉树中知道越到后面递归的次数越多,最下面的一层是占总的约一半,而快速排序也有这样的问题,在区间小的时候递归会非常多,所以在小区间就可以用其他的排序方法来代替,但区间小于一个范围时可以采用插入排序来排。
代码实现:
void QuickSort(int* a,int left, int right)
{if (left >= right)return;if ((right - left + 1) < 10){InsertSort(a+left, right - left + 1);}else{int begin = left;int end = right;int keyi = GetMidi(a, left, right);while (begin < end){while (begin < end && a[keyi] <= a[end]){--end;}while (begin < end && a[keyi] >= a[begin]){++begin;}swap(&a[begin], &a[end]);}swap(&a[keyi], &a[begin]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}}
这里需要注意的是用插入排序时参数应该是a+left而不是a,因为在递归过程中数组已经被分成很多个区间了(逻辑上),插入排序的是指定位置且指定大小排。
4.关于快速排序的细节
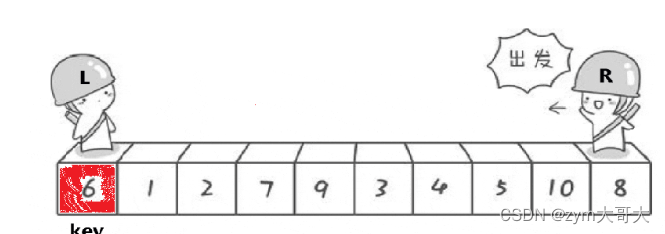
在代码实现里是让R先走的,R停下来才到L走,都停下来才交换,最后在交换L和key的值,为什么key的值一定比L与R相遇的位置对应的值小呢?
下面是分析:
1.L遇R:R先走然后找到了比key小的值停下来了,L开始走,但是没有找到比key大的值,最后于R相遇,此时相遇的地方对应的值是比key小的。
2.R遇L:R找到比key小的值停下来,L也遇到比key大的值停下来了,然后交换,此时R继续走,但是没有找到比key小的值了,就会一直走与L相遇,此时L所在的位置是上一次交换完的位置,也就是说L的位置的值原本是在R上一次停下来的位置对应的值,而这个值是一定比key小的,不然R是不会停下来的。
综上可知,最后L所在的位置是一定小于key对应的值的。
5.总代码:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tmp;}
}
int GetMidi(int*a,int left, int right)
{int midi = (left + right) / 2;if (a[midi] < a[right]){if (a[midi] > a[left]){return midi;}else{if (a[left] > a[right])return right;elsereturn left;}}else//a[midi]>a[right]{if (a[midi] > a[left]){if (a[right] > a[left])return right;elsereturn left;}elsereturn midi;}
}
void QuickSort(int* a,int left, int right)
{if (left >= right)return;if ((right - left + 1) < 10){InsertSort(a+left, right - left + 1);}else{int begin = left;int end = right;int keyi = GetMidi(a, left, right);while (begin < end){while (begin < end && a[keyi] <= a[end]){--end;}while (begin < end && a[keyi] >= a[begin]){++begin;}swap(&a[begin], &a[end]);}swap(&a[keyi], &a[begin]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}}void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){// Öظ´²»¶àa1[i] = rand() + i;// Öظ´½Ï¶à//a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin5 = clock();QuickSort(a1, 0, N - 1);int end5 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("QuickSort:%d\n", end5 - begin5);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{int arr[] = { 11,7,5,9,6,1,4,3,8,8,8,101 };int size = sizeof(arr) / sizeof(arr[0]);//TestOP();//InsertSort(arr, size);QuickSort(arr,0,size-1);for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
}这篇关于快速排序(排序中篇)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







