多源 BFS 详解

本文主要是介绍多源 BFS 详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、多源与单源的区别

二、例题练习

2.1 例题1：01 矩阵

2.2 例题2：飞地的数量

2.3 例题3：地图中的最高点

2.4 例题4：地图分析

一、多源与单源的区别

单源最短路问题如何解决已经在上篇博客给出BFS 解决最短路问题，如果还没学习单源的建议先学习，因为多源就是在单源的基础上进行一些改动即可，即把多个源点一起放入队列中。

• 注意：

多源 BFS 只能用来解决边权为 1 （其实只要边权相等即可，可以转化为边权 1 来解决）的多源最短路问题。如果是边权不相等的情况那么就要使用到图论里面的 Floyd-Warshall 算法，这个后续会写到。

• 那么该如何解决多源 BFS 问题呢？

解法1：暴力，直接把多源最短路问题转化为若干个单源最短路问题，这个大概率是会超时的，因为重复查找的次数非常多。

解法2：把所有的源点当成一个 “超级源点”，那么问题就变成了单一的单源最短路问题。

• 如何证明正确性呢？

理性：严格的证明，这些在一些算法书上能够找到，比较麻烦，文章主要写，如何来做题。故我们就感性的理解一下。

感性：就好比如下图这些性能相同的汽车（把汽车看成开始的源点），如果采用单源最短路的解决思路就是一辆一辆车启动，最后比较谁先到终点。如果采用多源最短路的解题思路就是把这些车一起启动，谁先到终点，就是最短路。这里可能有的友友会问，这样和单源最短路的时间复杂度不是一样的嘛？其实当在同一条路上如果有节点在前面，那么后面的节点就可以直接舍去，因为绝对不可能是最短路。

二、例题练习

2.1 例题1：01 矩阵

• 题目链接：01 矩阵

• 问题描述：

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

• 解题思路：

如果采用单源最短路（一个位置一个位置的去求）的话会超时（替大家试过了），正确的解法多源 BFS + 正难则反（填表更快），把所有的 0 当成起点，1当作终点（终点可以有多个）。找到一个 1 且是没有被遍历过的就可以把路径数直接填入，因为绝对没有比这个更小的路径了。

• 代码编写：

直接把最开始创建的数组都初始化成 -1 ，这样就不用创建一个 vis 表来标记已经走过的节点。且路径数可以直接在原来的路径数上 + 1 即可，一举两得。具体代码如下：

class Solution {int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};public int[][] updateMatrix(int[][] mat) {//1.把所有为0的元素存入队列int n = mat.length;int m = mat[0].length;//2.创建 dest 数组//3.dest初始化为 - 1int[][] dest = new int[n][m];for(int i = 0;i < n;i++){Arrays.fill(dest[i],-1);}Queue<int[]> q = new LinkedList<>();for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){if(mat[i][j] == 0){dest[i][j] = 0;q.add(new int[]{i,j});}}}//4.bfswhile(!q.isEmpty()){int[] tmp = q.poll();int a = tmp[0],b = tmp[1];for(int k = 0;k < 4;k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && dest[x][y] == -1){if(mat[x][y] == 1){//5.在原来的基础上直接 + 1dest[x][y] = dest[a][b] + 1;}q.add(new int[]{x,y});}}}return dest;}
}

2.2 例题2：飞地的数量

• 题目链接：飞地的数量

• 问题描述：

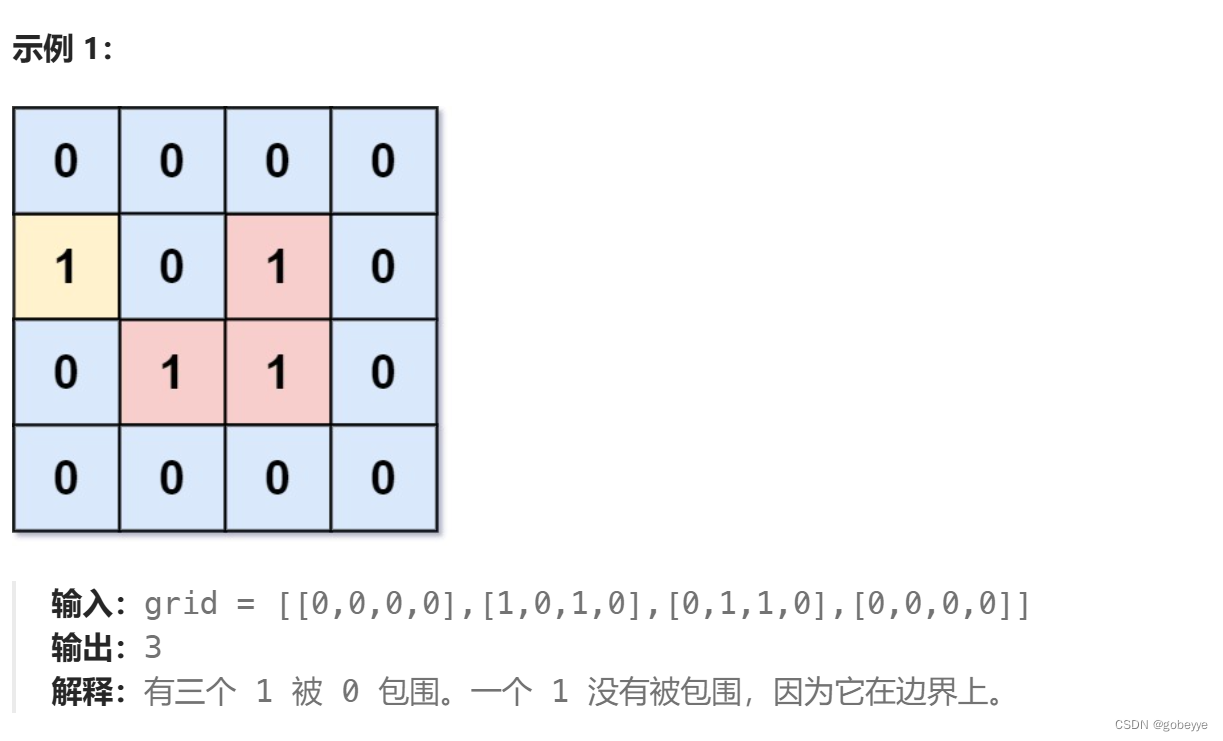
给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

• 解题思路：

正难则反：从边上的 1 开始搜索，把与边上 1 相连的联通区域全部标记⼀下，然后再遍历⼀遍矩阵，看看哪些位置的 1 没有被标记即可，标记的时候，可以用多源 bfs 解决（这题单源或者 DFS都行）。

• 代码编写：

class Solution {int n,m;int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};public int numEnclaves(int[][] grid) {n = grid.length;m = grid[0].length;//1.拿所有边界的1进行一次bfs标记Queue<int[]> q = new LinkedList<>();for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){if(i == 0 || i == n - 1 || j == 0 || j == m - 1){//这么写比较快且不容易出错if(grid[i][j] == 1){q.add(new int[]{i,j});}}}}//直接改为2即可while(!q.isEmpty()){int size = q.size();for(int i = 0;i < size;i++){int[] tmp = q.poll();int a = tmp[0],b = tmp[1];grid[a][b] = 2;for(int k = 0;k < 4;k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == 1){q.add(new int[]{x,y});grid[x][y] = 2;}}}}//2.最后遍历如果为 1 且未被标记的话ret++int ret = 0;//最后的结果for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){if(grid[i][j] == 1){ret++;}}}//3.返回 retreturn ret;}
}

2.3 例题3：地图中的最高点

• 题目链接：地图中的最高点

• 问题描述：

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由陆地和水域单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个陆地格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个水域格子。

你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是水域，那么它的高度必须为 0 。
任意相邻的格子高度差至多为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值最大。

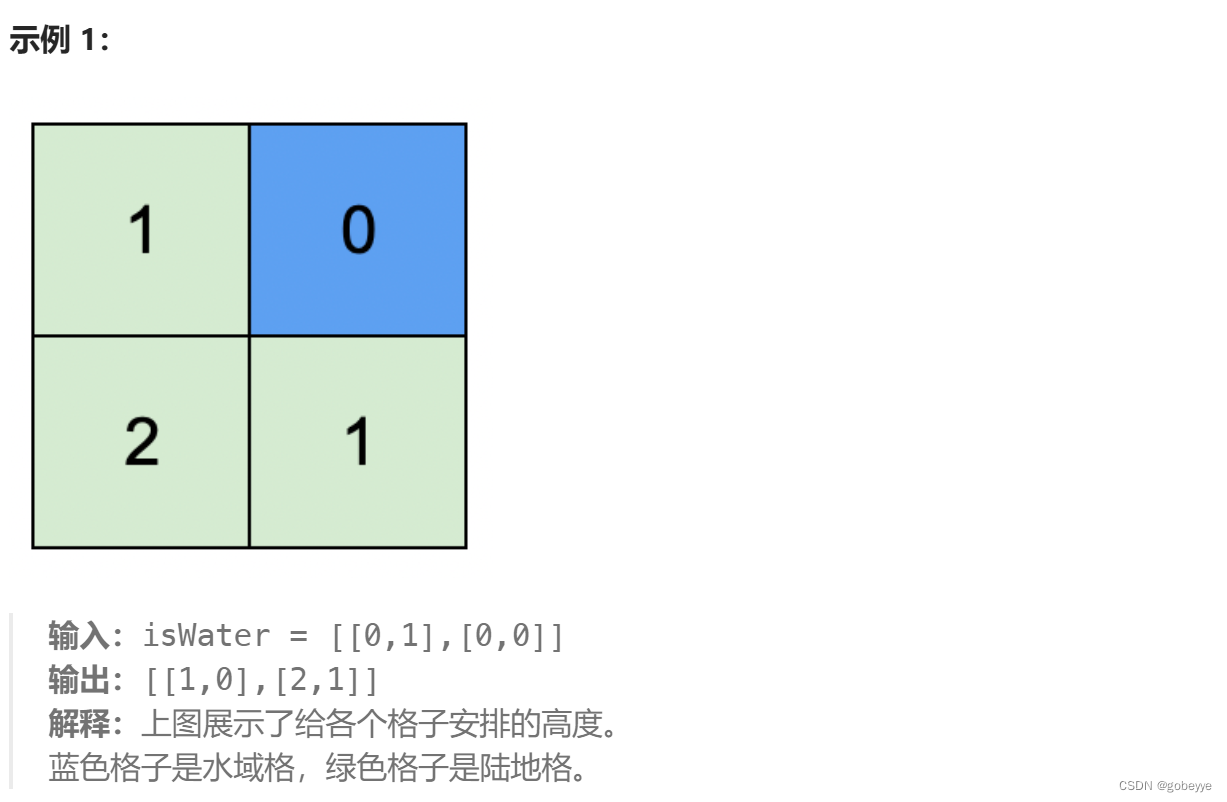
请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

• 解题思路：

01矩阵的变型题，直接用多源 bfs 解决即可。任意相邻的格子高度差至多为 1，这个条件非常重要，因为有这个条件我们才能确定这题其实是用最短路的思路来解决。具体就是把所有水域的格子添加到队列中，一层一层遍历即可。

• 代码编写：

class Solution {int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};public int[][] highestPeak(int[][] isWater) {//多源 bfsint n = isWater.length;int m = isWater[0].length;int[][] ans = new int[n][m];//3.把返回数组初始化为 -1for(int i = 0;i < n;i++){Arrays.fill(ans[i],-1);}//1.找到所有的值为 1 的加入 bfsQueue<int[]> q = new LinkedList<>();for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){if(isWater[i][j] == 1){ans[i][j] = 0;q.add(new int[]{i,j});}}}while(!q.isEmpty()){int size = q.size();for(int i = 0;i < size;i++){int[] tmp = q.poll();int a = tmp[0],b = tmp[1];//这个地方不用再填值了for(int k = 0;k < 4;k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && ans[x][y] == -1 && isWater[x][y] == 0){ans[x][y] = ans[a][b] + 1;//直接在原来的数值上 + 1 即可//不用再来一个timeq.add(new int[]{x,y});}}}}//4.返回答案return ans;}
}

2.4 例题4：地图分析

• 题目链接：地图分析

• 问题描述：

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

• 解题思路：

正难则反，把所有 1 的节点都进队，这样一次就可以把所有的 0 都填好（路径数）。和上面几题都差不多，多源 BFS 代码编写倒是不难，主要是要先转化一下，怎么把那么多节点变成 “超级源点”。

• 代码编写：

class Solution {int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};public int maxDistance(int[][] grid) {//多源 bfsint n = grid.length;int m = grid[0].length;boolean[][] vis = new boolean[n][m];//1.把 1 进 bfsQueue<int[]> q = new LinkedList<>();for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){if(grid[i][j] == 1){q.add(new int[]{i,j});}}}if(q.size() == 0 || q.size() == (n * m)){return -1;}int time = 0;//2.time计数while(!q.isEmpty()){int size = q.size();time++;for(int i = 0;i < size;i++){int[] tmp = q.poll();int a = tmp[0],b = tmp[1];vis[a][b] = true;for(int k = 0;k < 4;k++){int x = a + dx[k],y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && !vis[x][y] && grid[x][y] == 0){q.add(new int[]{x,y});//3.vis 去重vis[x][y] = true;}}}}return time - 1;}
}