第五十五周：文献阅读

2024-06-02 12:20
文章标签 阅读 文献 第五十五

本文主要是介绍第五十五周：文献阅读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

摘要

Abstract

文献阅读：基于VMD和深度学习的PM2.5浓度混合优化预测模型研究

 一、现有问题

二、提出方法

 三、方法论

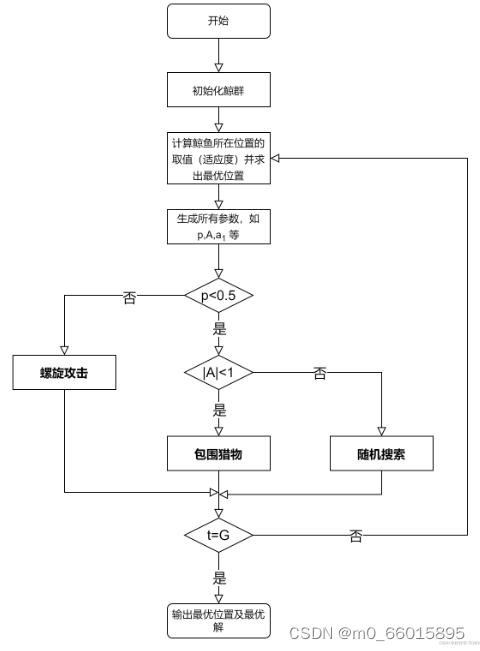
1. 鲸优化算法（WOA）

2. 变分模式分解（VMD）

3.WOA-VMD优化方法

4. 双向长期记忆神经网络（BiLSTM）

四、所提的方法（WOA-VMD-BiLSTM模型）

五、研究实验

1. 数据集

2.评估指标

3.实验过程

4. 实验结果

六、代码实现

总结

摘要

本周阅读的文献《A hybrid optimization prediction model for PM2.5 based on VMD and
deep learning》中提出了本文一种新的混合优化预测模型WOA-VMD-BiLSTM模型，预测大气中的PM2.5浓度。该模型结合了鲸鱼优化算法(WOA)、变分模态分解(VMD)和双向长短期记忆神经网络(BiLSTM)。针对PM2.5数据的强非线性特征，首先，使用WOA对VMD的参数进行优化，接着，经过优化的VMD对PM2.5序列进行分解，将其转化为一系列固有模态函数(IMF)；最后BiLSTM网络被用来捕捉每个IMF的非线性和时间序列特性，所有特征融合后生成最终的PM2.5浓度预测。实验结果显示，模型不仅在短期预测中表现出优越性，还能成功捕捉PM2.5浓度的长期变化趋势。

Abstract

The literature "A hybrid optimization prediction model for PM2.5 based on VMD and deep learning" read this week proposes a new hybrid optimization prediction model, WOA-VMD-BiLSTM, to predict PM2.5 concentrations in the atmosphere. This model combines Whale Optimization Algorithm (WOA), Variational Mode Decomposition (VMD), and Bidirectional Long Short Term Memory Neural Network (BiLSTM). Regarding the strong nonlinear characteristics of PM2.5 data, first, WOA is used to optimize the parameters of VMD. Then, the optimized VMD decomposes the PM2.5 sequence into a series of intrinsic mode functions (IMFs); Finally, the BiLSTM network was used to capture the nonlinear and time series characteristics of each IMF, and all features were fused to generate the final PM2.5 concentration prediction. The experimental results show that the model not only demonstrates superiority in short-term prediction, but also successfully captures the long-term trend of PM2.5 concentration changes.

文献阅读：基于VMD和深度学习的PM2.5浓度混合优化预测模型研究

A hybrid optimization prediction model for PM2.5 based on VMD and deep learningicon-default.png?t=N7T8https://doi.org/10.1016/j.apr.2024.102152PDF：A hybrid optimization prediction model for PM2.5 based on VMD and deep learning (sciencedirectassets.com)

 一、现有问题

  1. PM2.5数据序列具有强烈的非线性特征，传统预测方法难以精确捕捉这些特征，导致预测精度不高。
  2. 在深度学习模型中LSTM模型可以有效地捕获PM2.5浓度的变化，然而LSTM受限于顺序处理输入数据，不能充分利用PM2.5序列前后的信息。
  3. EMD存在严重的模态混叠问题，缺乏坚实的数学基础。

二、提出方法

针对上述问题，本文提出了一个基于鲸鱼优化算法(WOA)、变分模态分解(VMD)以及双向长短期记忆神经网络(BiLSTM)的混合优化预测模型——WOA-VMD-BiLSTM模型。该模型通过优化VMD参数，有效分解PM2.5序列数据，提取非线性及时间序列特征，以提高预测准确性。

 三、方法论

1. 鲸优化算法（WOA）

WOA是一种基于座头鲸捕食行为启发的群体智能优化算法，以其结构简单、易于实施且强大的寻优能力受到国内外研究者的青睐。算法通过模拟座头鲸的围猎策略，生成圆形或“9”形路径包围猎物，寻找问题的最优解。

鲸鱼优化算法由三部分动作组成：包围猎物、螺旋攻击猎物（发泡网攻击）、随机搜索猎物。WOA算法将当前最优候选解做为目标猎物（最优解），在知道猎物位置后鲸群开始根据当前自身与猎物位置的关系更新位置。为模拟座头鲸的螺旋过程，也就是发泡网攻击过程，我们在鲸鱼与猎物之间建立一种螺旋方程，模拟座头鲸的螺旋状运动，包围猎物和螺旋攻击，这两种行为的选择是通过随机的方式选择的，当概率p<0.5时选择包围猎物，反之则选择螺旋攻击。

2. 变分模式分解（VMD）

VMD的作用是将构成一个信号的多个子信号分解出来。如下图所示，信号(a)经过VMD后分解成了三个模态(也即三个子信号)，这三个模态正是构成信号(a)的三个子信号。

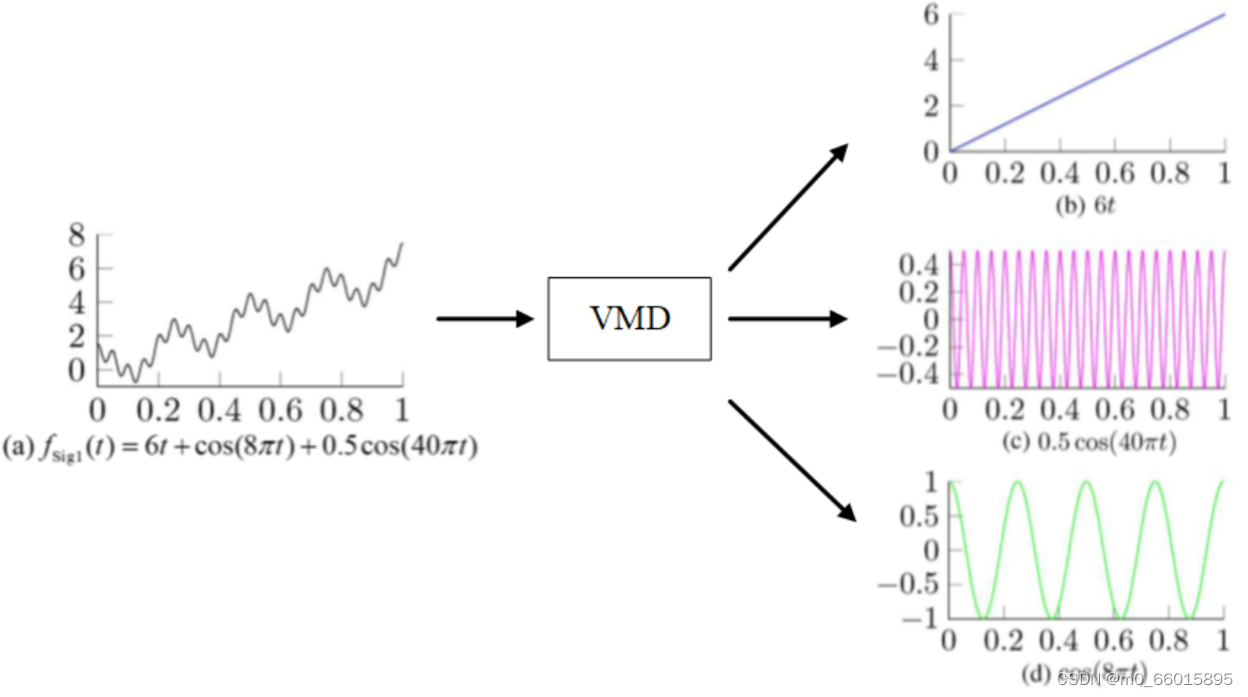
9bb64228b201432192324ed6a7ae9ba2.png

变分模态分解可以很好抑制EMD方法的模态混叠现象（通过控制带宽来避免混叠现象）。与EMD原理不同，该方法假设任何的信号都是由一系列具有特定中心频率、有限带宽的子信号组成（即IMF）。通过对变分问题进行求解，得到 中心频率与带宽限制，找到 各中心频率在频域中对应的有效成分，得到模态函数。VMD 的分解过程就是变分问题的求解过程，其算法主要包括 变分问题的构造和 变分问题的求解。

VMD的求解过程主要包含两点约束：

  1. 要求每个模态分量中心频率的带宽之和最小；
  2. 所有的模态分量之和等于原始信号。

变分问题的构造

所谓变分问题，就是求泛函的极值。在VMD中，泛函指的是VMD约束变分模型，而要求的极值，就是“每个模态分量中心频率的带宽之和最小”。 

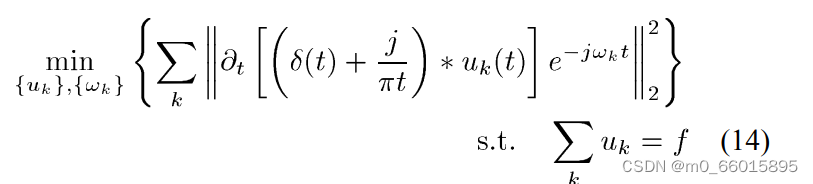
dce67cc3fe3c4703815912da89891a55.png

上式表示的变分问题，即求取“每个模态分量中心频率的带宽之和最小”时的模态函数eq?u_%7Bk%7D和中心频率eq?w_%7Bk%7D，其中eq?u_%7Bk%7D%3D%5Cbegin%7BBmatrix%7D%20u_%7B1%7D%2Cu_%7B2%7D%2C...%2Cu_%7Bk%7D%20%5Cend%7BBmatrix%7D、eq?w_%7Bk%7D%3D%5Cbegin%7BBmatrix%7D%20w_%7B1%7D%2Cw_%7B2%7D%2C...%2Cw_%7Bk%7D%20%5Cend%7BBmatrix%7D。 

变分问题的求解

利用二次惩罚项和拉格朗日乘子法的优势，引入了增广拉格朗日函数，将上述约束变分问题转变为非约束变分问题，其中，eq?%5Calpha是罚参数，eq?%5Clambda是Lagrangian乘子。

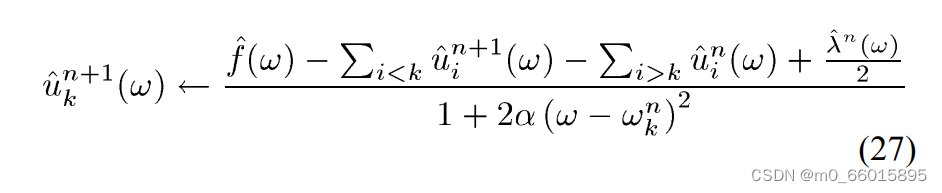
ac7fd2da946b454285211adb234dba1f.png

首先初始化eq?u_%7Bk%7D 、eq?w_%7Bk%7D、eq?%5Clambda，然后通过迭代对于所有eq?%5Comega%20%5Cgeq%200，根据VMD算法公式更新eq?u_%7Bk%7D 和 eq?w_%7Bk%7D

更新模态函数eq?u_%7Bk%7D：

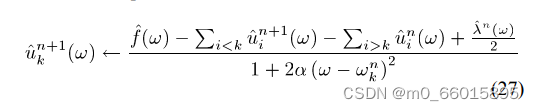
1197b1b2f9c84009ac967a479601ea77.png

更新中心频率eq?w_%7Bk%7D：

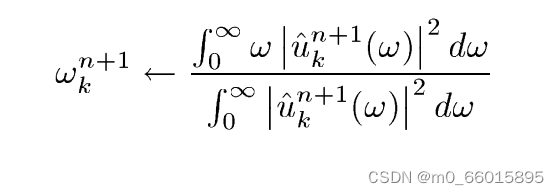
a3366963863c42498cc90660e4a07c73.png

 根据相关的算法更新拉格朗日乘数eq?%5Clambda

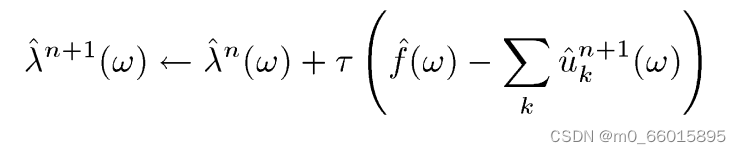
b240ce1c26ec403986021e09b1ed70af.png

不断重复更新直到满足下面的迭代约束条件，即对于所有的eq?%5Comega%20%5Cgeq%200，解析信号的单边谱只包含非负频率。

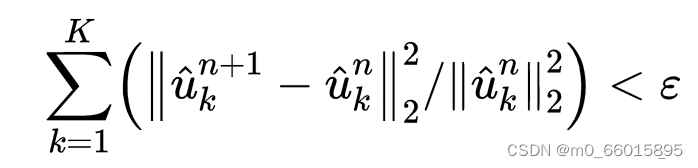
1bf06cf637814c4bae7492fe10ce2d52.png

则停止迭代，否则继续迭代更新三个参数的值，以上便是求解每一个模态的单步骤。

相比较EMD：

  1. 相对于EMD，VMD对采样和噪声具有更强的鲁棒性。
  2. 相对于EMD，VMD在分解复杂信号方面效果更好。
  3. VMD技术具有可以确定模态分解个数的优点，其自适应性表现在根据实际情况确定所给序列的模态分解个数。

VMD可以分解获得包含多个不同频率尺度且相对平稳的模态（子序列），适用于非平稳性的序列。能够将原始的PM2.5数据序列分解为多个内在模态函数(IMF)，有效降低原始数据的非线性，增强信号稳定性，便于后续特征提取。

3.WOA-VMD优化方法

在进行VMD分解之前，通常需要合理地设置模式数K和惩罚因子α。考虑到VMD分解参数选择对结果影响大且手动选择成本高，采用WOA优化VMD的模态数量K和惩罚因子α。通过设定合适的参数范围并利用WOA最小化包络熵作为适应度函数，自动找到最佳参数组合。

  1. 设定VMD的参数K和α的取值范围，初始化WOA的种群规模、迭代次数和空间维数等相关参数。
  2. 执行VMD分解，并根据每个个体在初始种群中的位置计算适应度值。
  3. 根据适应度值，更新鲸鱼个体的位置，并保留相应的参数组合。
  4. 新周期的起始种群是更新后的鲸鱼种群，如果当前迭代过程达到最大迭代次数，则转到步骤5。如果没有转到步骤2。
  5. 获得参数[K，α]的最优组合。

4. 双向长期记忆神经网络（BiLSTM）

LSTM作为RNN的一种变体，能够有效地控制和维护时间步之间的信息流，从而克服梯度消失的问题，同时具有从时间序列数据中提取长期关系的能力。实际上，PM2.5受多种因素影响，包括过去的气象条件和污染源的排放。这些因素不仅影响当前时刻的PM2.5浓度，还可能对未来浓度产生影响。另一方面，BiLSTM在LSTM之上引入了双向结构，使BiLSTM能够有效地捕获当前时间点的前向和后向特征，这种双向结构使模型能够更全面地理解和建模PM2.5数据中的时间依赖性，从而提高识别和预测特定时间模式的精度。

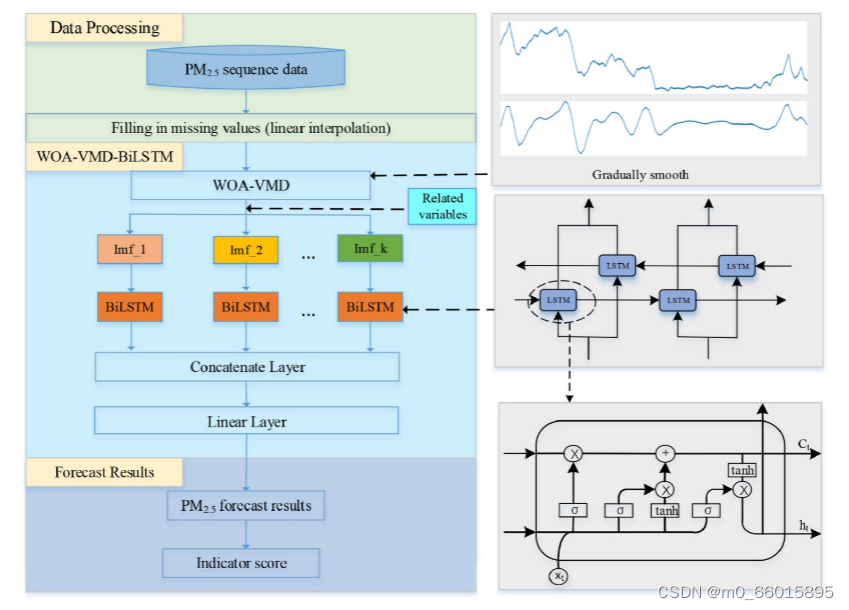
四、所提的方法（WOA-VMD-BiLSTM模型）

该模型首先利用WOA优化的VMD对PM2.5序列进行分解，得到多个IMF，然后用BiLSTM捕捉每个IMF的非线性和时间序列特征，最后融合所有特征进行PM2.5浓度预测。实验表明，与基线模型相比，该模型显著提高了短时预测精度，同时也能较好地捕捉长期趋势变化。

  1. PM2.5数据线性插值后，输入WOA-VMD方法，用于确定VMD分解的最佳模式数和相应的惩罚因子。
  2. PM2.5的原始时间序列被分解成一些平滑的IMF使用VMD。
  3. 联合收割机将与PM2.5相关的各种变量组合为每个IMF。
  4. BiLSTM用于学习每个IMF的非线性和时间特征。
  5. 最后，融合学习到的各部分特征，生成PM2.5浓度预测结果。

五、研究实验

1. 数据集

实验部分使用了UCI提供的北京PM2. 5数据和中国五个城市的PM2. 5数据，这两个数据都是每小时采集的，均为多变量时间序列数据，时间跨度分别为2010年至2014年和2015年。数据主要有两种类型：气象数据和PM2.5污染物数据，其中包含PM2.5值、温度和风向等不同属性。

2.评估指标

用决定系数（R2）、平均绝对误差（RMSE）和均方根误差（MAE）评价模型的预测效果。而RMSE和MAE用于测量预测值和真实的值之间的误差，两者中任一个的较低值指示预测更接近真实值并且误差更小。R2用于测量预测值和真实的值之间的拟合度，R2越接近1，与数据的拟合度越好。

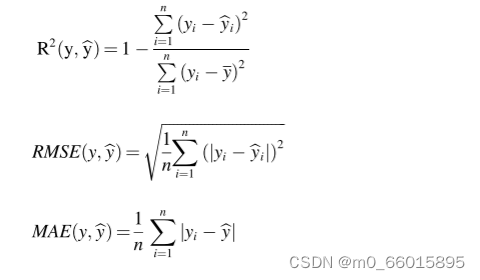
3.实验过程

模型训练前，数据预处理包括缺失值处理、异常值去除、标准化，按时间分割训练/测试集划分。训练过程涉及超参数调优，选择最优模型。

4. 实验结果

一、WOA-VMD分解结果及有效性验证

实验展示了鲸鱼优化算法（WOA）与变分模态分解（VMD）相结合（WOA-VMD）在处理PM2.5数据序列时的分解效果。通过对北京、成都、广州和沈阳四个城市的数据应用WOA-VMD，观察到迭代曲线有效地调整了VMD的分解参数。这些优化后的参数组合在不同城市中表现出了稳定且高效的分解性能，例如北京的K=4, α=20.5，这证实了WOA-VMD在参数优化上的有效性，有助于提升分解质量和后续预测的准确性。

二、单步预测与多步预测

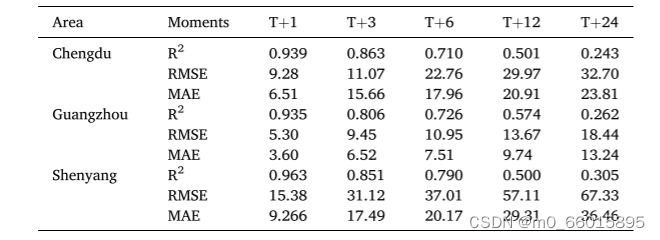
在单一时间步预测结果的分析中，与多层感知器（MLP）、循环神经网络（RNN）、长短期记忆网络（LSTM）和双向LSTM（BiLSTM）等四类深度学习基线模型对比，WOA-VMD-BiLSTM混合模型表现出显著优势。特别是，与最好的基线模型BiLSTM相比，提出模型在预测精度上有明显提升，如在T+12时刻，R2提高了0.28，平均绝对误差（MAE）和均方根误差（RMSE）分别降低了15.04和20.55。这直接证明了WOA-VMD方法的有效性，并表明即使是短期预测，模型也能保持较高精度。

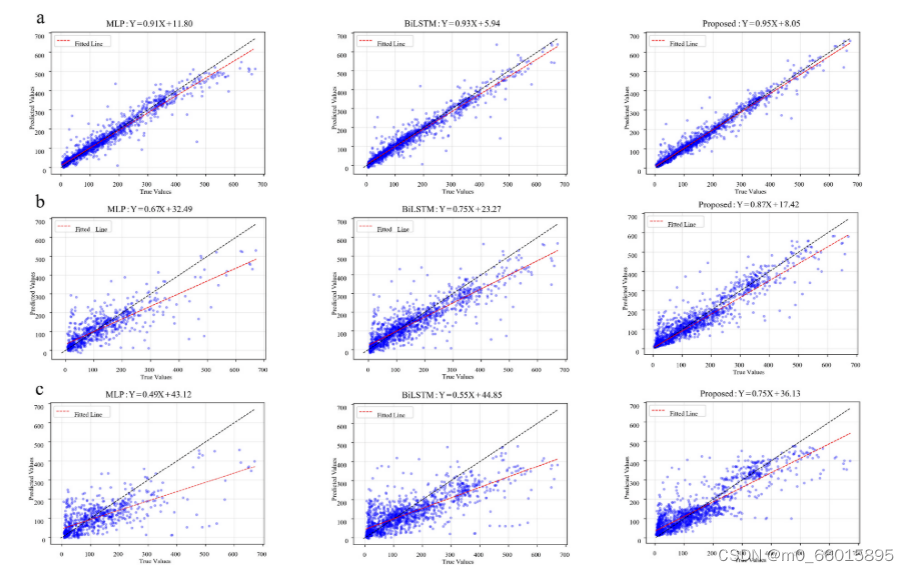
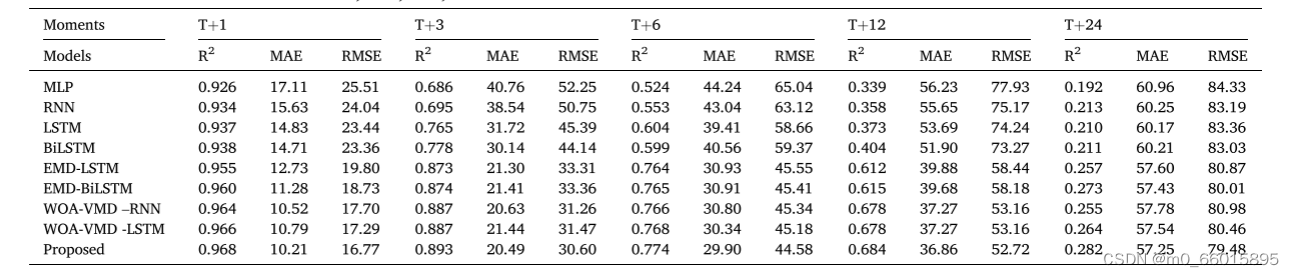
对于多步预测结果的分析，无论是短期（1~6小时）、中期（7~12小时）还是长期（13~24小时）预测，WOA-VMD-BiLSTM模型相比基线模型都有明显的性能提升。在1~6小时和7~12小时内，模型的RMSE至少分别减少18.12和20.17，而与结合经验模态分解（EMD）的混合模型相比，减少量也分别至少为2.33和4.73。即便是预测时间延长至24小时，模型仍能维持与其他混合模型的性能差距，体现了其在长时预测上捕捉趋势的能力。

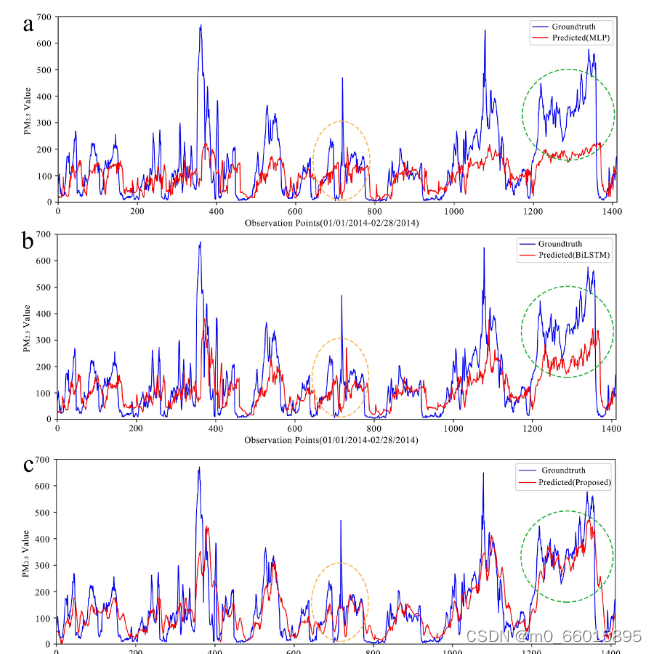
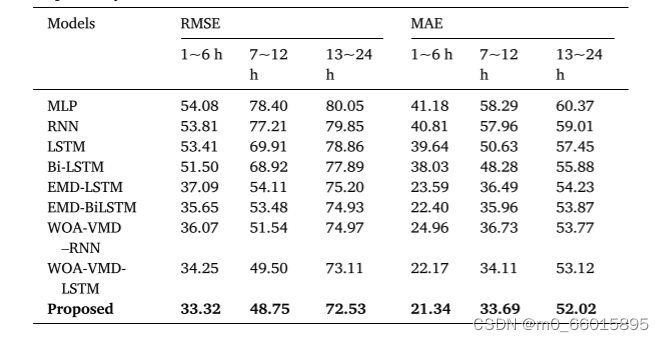
三、泛化性评估

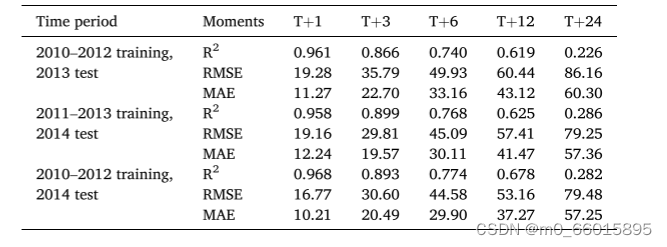
为了评估模型的泛化能力，从时间和空间两个维度进行了验证。时间上，通过改变训练和测试数据集的时间段，发现模型在不同时间段的预测性能仍然稳定，如在北京PM2.5数据中，T+1时刻的R2高达0.968，即使在T+12时刻，R2仍有0.678，显示了模型对短期和中期预测的稳定准确度。空间上，利用来自中国五个城市的数据，模型同样展现出了良好的适应性，说明其在不同地理环境下预测PM2.5浓度的可靠性，这对于实际应用中推广至不同城市和区域的空气质量预测具有重要意义。

六、代码实现

WOA算法

 定义了一个WhaleOptimizationAlgorithm类，实现了WOA的主要逻辑。在optimize方法中，每个迭代周期内，每只鲸鱼根据随机生成的参数A和C，使用search_prey和encircle_prey方法更新自己的位置，同时检查更新后的位置是否在搜索空间内（通过np.clip实现）。如果更新后的解更优，则更新全局最优解。最后输出迭代过程中的最佳解及其适应度值。

import numpy as np
import randomclass WhaleOptimizationAlgorithm:def __init__(self, func, dim, lb, ub, n_whales=30, max_iter=100, a=2, l=2):self.func = func  # 目标函数self.dim = dim  # 维度self.lb = lb  # 下界self.ub = ub  # 上界self.n_whales = n_whales  # 鲸鱼数量self.max_iter = max_iter  # 最大迭代次数self.a = a  # 控制搜索范围的参数self.l = l  # 更新位置的步长参数self.population = np.random.uniform(lb, ub, (n_whales, dim))  # 初始化种群self.best_solution = self.population[np.argmin([self.func(x) for x in self.population])]  # 最佳解决方案初始化self.best_fitness = self.func(self.best_solution)  # 最佳适应度初始化def search_prey(self, A, C, X_prey, X_star):"""鲸鱼搜索猎物的位置更新公式"""D = abs(C * X_prey - X_star - A * np.ones_like(X_prey))X_new = X_star - A * Dreturn np.clip(X_new, self.lb, self.ub)def encircle_prey(self, X, X_star):"""鲸鱼围猎行为，螺旋更新位置"""r1 = random.random()A = 2 * a * r1 - al = 2 * r1b = 1D = abs(X - X_star)X_new = X_star - A * D + b * l * ((np.abs(np.random.rand(*D.shape) * D - D)) / 2)return np.clip(X_new, self.lb, self.ub)def optimize(self):for t in range(self.max_iter):for i in range(self.n_whales):A = 2 * np.random.rand() * self.a - self.ar = np.random.rand()C = 2 * rif r < 0.5:self.population[i] = self.search_prey(A, C, self.population[i], self.best_solution)else:self.population[i] = self.encircle_prey(self.population[i], self.best_solution)fitness_i = self.func(self.population[i])if fitness_i < self.best_fitness:self.best_solution = self.population[i].copy()self.best_fitness = fitness_iprint(f"Iteration {t+1}, Best Fitness: {self.best_fitness}")return self.best_solution, self.best_fitness# 示例目标函数，比如最小化某个复杂函数
def objective_function(x):return np.sum(x**2)  # 以求解x^2的最小值为例# 设置参数并运行WOA
woa = WhaleOptimizationAlgorithm(objective_function, dim=2, lb=-10, ub=10, max_iter=100)
best_solution, best_fitness = woa.optimize()
print("Best Solution:", best_solution, "Best Fitness:", best_fitness)

VMD分解

#函数定义: VMD函数接收输入数据data，正则化参数alpha，要提取的模态数K，时间尺度分离数组tau，以及最大迭代次数iter_num。
def VMD(data, alpha, K, tau, iter_num):N = len(data)#创建矩阵U和V作为随机初始化的模式向量，并计算频率矩阵omega。omega = np.linspace(0, 1/(2*np.pi*tau[0]), N)[:, None]U = np.random.randn(N, K)V = np.random.randn(N, K)#主循环进行多次迭代for _ in range(iter_num):U = np.dot(U, np.diag(1/np.sqrt(np.sum(U**2, axis=0))))V = np.dot(V, np.diag(1/np.sqrt(np.sum(V**2, axis=0))))#正交化：利用对角矩阵来规范化U和V，确保它们的范数接近单位长度。U = np.dot(data, V) + alpha * UV = np.dot(data, U.T) + alpha * V#更新：通过乘积运算更新U和V，同时加上正则项alpha * U和alpha * V来避免过拟合U = np.dot(U, np.diag(1/np.sqrt(np.sum(U**2, axis=0))))V = np.dot(V, np.diag(1/np.sqrt(np.sum(V**2, axis=0))))#再次正交化：迭代后再次正交化U和VU = np.dot(U, np.diag(np.exp(-1j * np.outer(omega, tau))))V = np.dot(V, np.diag(np.exp(1j * np.outer(omega, tau))))#调整频率：对U和V进行复数旋转，引入时间尺度信息。modes = np.real(np.dot(data, V))#计算最终的模态（IMFs）通过数据与规范化后的V矩阵的乘积，并取实部。return modes

BiLSTM 

# 构建BiLSTM模型
def build_bilstm_model(input_shape):model = Sequential()model.add(Bidirectional(LSTM(units=64, input_shape=input_shape, return_sequences=True)))model.add(Bidirectional(LSTM(units=32))model.add(Dense(1))  # 假设单输出，即PM2.5浓度model.compile(optimizer='adam', loss='mse')return model

主函数

if __name__ == "__main__":data_path = 'pm25_data.csv'train_data, test_data = preprocess_data(data_path)# 定义参数alpha = 1e-6  # Regularization parameter to avoid singularityK = 3       # Number of IMFs to extracttau = np.linspace(1, 10, K)  # Time scales for each modeiter_num = 200  # Number of iterations for convergence# 通过WOA获取最优参数K, alpha = whale_optimization(range(2, 6), range(1, 100), 100)# 应用VMDimfs_train = variational_modal_decomposition(train_data, K, alpha)imfs_test = variational_modal_decomposition(test_data, K, alpha)# 准备BiLSTM输入，假设只用第一个IMFbilstm_input_shape = (imfs_train.shape[1], 1)model = build_bilstm_model(bilstm_input_shape)# 训练BiLSTM模型model.fit(imfs_train, train_data[:, 0], epochs=100, batch_size=32, validation_split=0.1)

 

总结

本文提出WOA-VMD-BiLSTM模型，模型结合了变分模态分解（VMD）、鲸鱼优化算法（WOA）和双向长短时记忆网络（BiLSTM）。VMD用于数据预处理，有效分解原始数据序列，降低非线性，提取多尺度信息。通过WOA优化VMD参数，模型能够更精准地学习PM2.5数据的非线性特征，分解出的固有模态函数（IMF）随后被BiLSTM网络利用，捕捉到每个IMF的复杂动态特征，克服手动调整的局限性，提升效率和预测精度，BiLSTM则捕捉序列的非线性和时间序列特征。模型在短、长期预测中均展现良好性能。

这篇关于第五十五周：文献阅读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1023959。

相关文章

JAVA智听未来一站式有声阅读平台听书系统小程序源码

JAVA智听未来一站式有声阅读平台听书系统小程序源码

智听未来，一站式有声阅读平台听书系统 🌟&nbsp;开篇：遇见未来，从“智听”开始 在这个快节奏的时代，你是否渴望在忙碌的间隙，找到一片属于自己的宁静角落？是否梦想着能随时随地，沉浸在知识的海洋，或是故事的奇幻世界里？今天，就让我带你一起探索“智听未来”——这一站式有声阅读平台听书系统，它正悄悄改变着我们的阅读方式，让未来触手可及！ 📚&nbsp;第一站：海量资源，应有尽有 走进“智听
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
软件架构模式：5 分钟阅读

软件架构模式：5 分钟阅读

原文： https://orkhanscience.medium.com/software-architecture-patterns-5-mins-read-e9e3c8eb47d2 软件架构模式：5 分钟阅读 当有人潜入软件工程世界时，有一天他需要学习软件架构模式的基础知识。当我刚接触编码时，我不知道从哪里获得简要介绍现有架构模式的资源，这样它就不会太详细和混乱，而是非常抽象和易
阅读更多...
【阅读文献】一个使用大语言模型的端到端语音概要

【阅读文献】一个使用大语言模型的端到端语音概要

摘要 ssum框架（Speech Summarization）为了 从说话人的语音提出对应的文本二题出。 ssum面临的挑战： 控制长语音的输入捕捉 the intricate cross-mdoel mapping 在长语音输入和短文本之间。 ssum端到端模型框架 使用 Q-Former 作为 语音和文本的中介连接 ，并且使用LLMs去从语音特征正确地产生文本。 采取 multi-st
阅读更多...
AI文献综述神器，有这一款就够了！

AI文献综述神器，有这一款就够了！

我是娜姐 @迪娜学姐 ，一个SCI医学期刊编辑，探索用AI工具提效论文写作和发表。 当前的AI辅助文献综述的工具有很多，如果说功能最强大的，娜姐无疑要推SciSpace了。 SciSpace利用强大的AI算法，理解并建立研究论文之间的联系，可以大大提升文献综述的质量和效率。并且其功能还在不断更新和完善。        1 强大的语义搜索功能 传统的关键词搜索可能会遗漏相关文献，Sc
阅读更多...
天然药物化学史话：“四大光谱”在天然产物结构鉴定中的应用-文献精读46

天然药物化学史话：“四大光谱”在天然产物结构鉴定中的应用-文献精读46

天然药物化学史话：“四大光谱”在天然产物结构鉴定中的应用，天然产物化学及其生物合成必备基础知识~ 摘要 天然产物化学研究在药物研发中起着非常重要的作用，结构研究又是天然产物化学研究中最重要的工作之一。在天然药物化学史话系列文章的基础上，对在天然产物结构研究中起绝对主导作用的“四大光谱”分析技术，即红外光谱、紫外光谱、质谱、核磁共振波谱在天然产物结构鉴定中的应用历史进行回顾与总结，并对其发展
阅读更多...
你读文献的方式可能错了！掌握这些技巧，让阅读事半功倍！

你读文献的方式可能错了！掌握这些技巧，让阅读事半功倍！

我是娜姐 @迪娜学姐 ，一个SCI医学期刊编辑，探索用AI工具提效论文写作和发表。 科研新手如何精读一篇论文？ 很多科研新手，一上来就疯狂下载几十上百篇文献。囫囵吞枣看完了，还是什么都不知道，大脑一片空白。究竟该如何读文献收获最大？ 大佬说，要积极阅读、频繁阅读。 什么是积极阅读？ 相比被动阅读，积极阅读是指在阅读之前准备好问题、设置阅读目标、保持批判性，收获更多、进步更大的一种阅读
阅读更多...
如何借助AI快速筛选和整理文献？

如何借助AI快速筛选和整理文献？

AIPaperGPT，论文写作神器~ https://www.aipapergpt.com/ 在撰写毕业论文时，文献综述是必不可少的部分。它不仅为你的研究提供理论背景，还展示了你对研究领域的深入理解。然而，文献综述的撰写过程常常让学生感到头疼，尤其是面对海量文献时，如何有效筛选、整理和撰写是一大难题。 本文将为大家介绍如何利用AI工具帮助你轻松高效地完成文献综述的写作。我们将详细讲解如何快速
阅读更多...
一键部署Phi 3.5 mini+vision！多模态阅读基准数据集MRR-Benchmark上线，含550个问答对

一键部署Phi 3.5 mini+vision！多模态阅读基准数据集MRR-Benchmark上线，含550个问答对

小模型又又又卷起来了！微软开源三连发！一口气发布了 Phi 3.5 针对不同任务的 3 个模型，并在多个基准上超越了其他同类模型。 其中 Phi-3.5-mini-instruct 专为内存或算力受限的设备推出，小参数也能展现出强大的推理能力，代码生成、多语言理解等任务信手拈来。而 Phi-3.5-vision-instruct 则是多模态领域的翘楚，能同时处理文本和视觉信息，图像理解、视频摘要
阅读更多...
深入理解计算机系统阅读笔记-第四章

深入理解计算机系统阅读笔记-第四章

第四章 处理器体系结构 一个处理器支持的指令和指令的字节级编码称为它的ISA(instruction-set architecture，指令集体系结构)。不同家族处理器有不同的ISA。ISA在编译器编写者和处理器设计人员之间提供了一个概念抽象层，编译器编写者只需要知道允许哪些指令，以及他们是如何编码的；而处理器设计者，必须建造出执行这些指令的处理器。 ISA模型看上去是顺序执行的，实际上同时处
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2