本文主要是介绍数学建模 —— 灰色系统(4),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
什么是灰色系统?
一、灰色关联分析
1.1 灰色关联分析模型
1.2 灰色关联因素和关联算子集
1.2.1 灰色关联因素
1.2.2 关联算子集
1.3 灰色关联公理与灰色关联度
1.3.1 灰色关联度
1.3.2 灰色关联度计算步骤
1.4 广义关联度
1.4.1 灰色绝对关联度
1.4.2 灰色相对关联度
1.4.3 灰色综合关联度
二、优势分析
2.1 灰色关联矩阵
2.2 几类灰色关联矩阵
2.3 系统优势关系
2.4 因素优势关系
2.5 系统准优势关系
2.6 准优特征与准优因素
三、生成数
3.1 累加生成数列
四、灰色模型(GM模型)
4.1 GM(1, 1)模型及定义
4.2 GM(1, 1)白化型
五、灰色预测
5.1 灰色预测的步骤
5.1.1 数据的检验与处理
5.1.2 建立模型
5.1.3 模型检验
5.2 数列预测
什么是灰色系统?
客观世界的很多实际问题,其内部的结构、参数以及特征并未全部被人们了解,人们不可能象研究白箱问题那样将其内部机理研究清楚,只能依据某种思维逻辑与推断来构造模型。对这类部分信息已知而部分信息未知的系统,我们称之为灰色系统。
一、灰色关联分析
1.1 灰色关联分析模型
根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间关联度就越大,反之就越小。
灰色关联分析方法弥补了采用数理统计方法作系统分析所导致的缺憾。它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。
1.2 灰色关联因素和关联算子集
1.2.1 灰色关联因素
(1)行为序列

(2)行为时间序列

(3)行为指标序列

(4)行为横向序列

1.2.2 关联算子集
(1)初值化算子

(2)均值化算子

(3)区间值化算子

(4)逆化算子

(5)倒数化算子

(6)关联因子空间

1.3 灰色关联公理与灰色关联度
1.3.1 灰色关联度

1.3.2 灰色关联度计算步骤

e.g.
clc, clear
a=[0.83 0.90 0.99 0.92 0.87 0.95
326 295 340 287 310 303
21 38 25 19 27 10
3.2 2.4 2.2 2.0 0.9 1.7
0.20 0.25 0.12 0.33 0.20 0.09
0.15 0.20 0.14 0.09 0.15 0.17
250 180 300 200 150 175
0.23 0.15 0.27 0.30 0.18 0.26
0.87 0.95 0.99 0.89 0.82 0.94];
for i=[1 5:9] %效益型指标标准化a(i,:)=(a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i=2:4 %成本型指标标准化a(i,:)=(max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end
[m,n]=size(a);
cankao=max(a')' %求参考序列的取值
t=repmat(cankao,[1,n])-a; %求参考序列与每一个序列的差
mmin=min(min(t)); %计算最小差
mmax=max(max(t)); %计算最大差
rho=0.5; %分辨系数
xishu=(mmin+rho*mmax)./(t+rho*mmax) %计算灰色关联系数
guanliandu=mean(xishu) %取等权重,计算关联度
[gsort,ind]=sort(guanliandu,'descend') %对关联度按照从大到小排序
1.4 广义关联度
三种关联度矩阵往往得出因素排序结果不完全相同,主要是因为绝对关联矩阵计算出的绝对关联序是从绝对量的角度考虑,相对关联矩阵得出的相对关联序是相对于原始点变化速率的角度考虑,而综合关联序是综合绝对量和相对变化速率的角度考虑,实际应用中,只要考虑绝对关联序即可。
1.4.1 灰色绝对关联度
(1)预备知识

(2)始点零化算子


(3)序列长度

(4)灰色绝对关联度


e.g.


(5)等时距序列
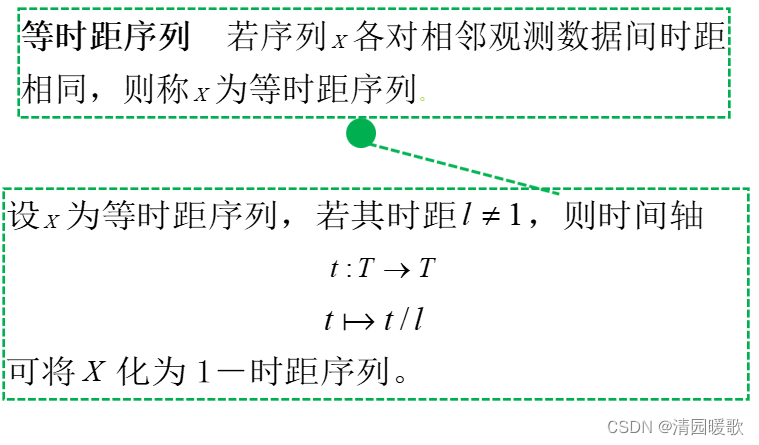
(6)1时距化

(7)灰色绝对关联度性质

1.4.2 灰色相对关联度
(1)定义和计算



(2)性质

1.4.3 灰色综合关联度
(1)概述


(2)性质

二、优势分析
2.1 灰色关联矩阵

2.2 几类灰色关联矩阵

2.3 系统优势关系

2.4 因素优势关系

2.5 系统准优势关系

2.6 准优特征与准优因素


| 关联度名称 | 准优特征 | 准优因素 |
| 绝对关联度 | ||
| 相对关联度 | ||
| 综合关联度 |
三、生成数
灰色系统理论把一切随机量都看作灰色数—即在指定范围内变化的所有白色数的全体。对灰色数的处理不是找概率分布或求统计规律,而是利用数据处理的办法去寻找数据间的规律。通过对数列中的数据进行处理,产生新的数列,以此来挖掘和寻找数的规律性的方法,叫做数的生成。数的生成方式有多种:累加生成、累减生成以及加权累加等等。这里主要介绍累加生成。
3.1 累加生成数列
把数列 x 各时刻数据依次累加的过程叫做累加过程,记作AGO,累加所得的新数列,叫做累加生成数列。

特点:
一般经济数列都是非负数列。累加生成能使任意非负数列、摆动的与非摆动的,转化为非减的、递增的。
四、灰色模型(GM模型)
灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程,进而用离散数据列建立微分方程形式的动态模型,由于这是本征灰色系统的基本模型,而且模型是近似的、非唯一的,故这种模型为灰色模型,记为GM(Grey Model),即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数,建立起的微分方程形式的模型,这样便于对其变化过程进行研究和描述。
4.1 GM(1, 1)模型及定义


4.2 GM(1, 1)白化型

值得注意的是:GM(1,1)的白化型(4)并不是由 GM(1,1)的灰微分方程直接推导出来的,它仅仅是一种“借用”或“白化默认”。
另一方面,GM(1,1)的白化型是一个真正的微分方程,如果白化型模型精度高,则表明所用数列建立的模型 GM(1,1)与真正的微分方程模型吻合较好,反之亦然。
五、灰色预测
灰色预测是指利用 GM 模型对系统行为特征的发展变化规律进行估计预测,同时也可以对行为特征的异常情况发生的时刻进行估计计算,以及对在特定时区内发生事件的未来时间分布情况做出研究等等。
这些工作实质上是将“随机过程”当作“灰色过程”, “随机变量”当作“灰变量”,并主要以灰色系统理论中的 GM(1,1)模型来进行处理。灰色预测在工业、农业、商业等经济领域,以及环境、社会和军事等领域中都有广泛的应用。特别是依据目前已有的数据对未来的发展趋势做出预测分析。
5.1 灰色预测的步骤
5.1.1 数据的检验与处理
首先,为了保证建模方法的可行性,需要对已知数据列做必要的检验处理。设参考数据为 ![]() ,计算数列的级比
,计算数列的级比
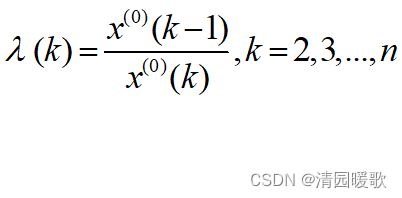
如果所有的 级比 ![]() 都落在可容覆盖
都落在可容覆盖
内,则数列 x(0) 可以作为模型 GM(1,1)的数据进行灰色预测。否则,需要对数列 x(0) 做必要的变换处理,使其落入可容覆盖内。
即取适当的常数c,作平移变换
y^(0) (k) = x^(0) (k) + c,k =1,2,…,n

5.1.2 建立模型
按灰色预测方法建立模型 GM(1,1),则可以得到预测值

5.1.3 模型检验
(1)残差检验准则
设:
![]()


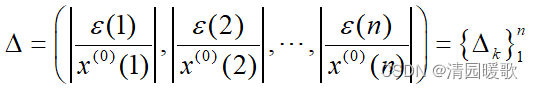

(2)关联度检验准则
设:
![]()


(3)均方差比与小误差检验准则


(4)精度等级参照表

5.2 数列预测
(1)定性分析
(2)引入适当的序列算子
(3)建立预测模型
(4)精度检验
(5)预测
(6)灰色决策模型
待续
这篇关于数学建模 —— 灰色系统(4)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







