TH方程学习（4）

本文主要是介绍TH方程学习（4），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、背景介绍

在本节将会对TH方程打包成一个函数，通过输入目标星的轨道要素，追踪星在目标星VVLH坐标系下的相对位置和速度，以及预报的时间，得到预报时刻追踪星在VVLH坐标系下的位置和速度，以及整个状态转移矩阵。

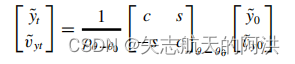
合并（1）（2），得到归一化形式的XZ方向的状态转移矩阵，（3），得到归一化形式的Y方向的状态转移矩阵。所以合并后的形式可以写为

根据归一化，可以写成的矩阵形式如下所示

根据式子

所以状态转移矩阵为

实现代码如下所示

function [rvt,Phi,rvt_phi] = TH_solver(ecc,Perigee,TA,delta_r,delta_v,t)
%TH_SOLVER 本函数旨在通过输入目标轨道的轨道要素，追踪星的初始相对位置和速度
%  输入
%  ecc    :  目标星的偏心率           0<ecc<1
%  Perigee:  目标星的近地点高度       (km)
%  TA     :  目标星的初始真近地点角   (deg) (0<TA<=360)
%  delta_r:  追踪星在目标星的VVLH位置 (km)
%  delta_v:  追踪星在目标星的VVLH速度 (km/s)
%  t      :  预报时间长度             (s)
%  输出
%  rvt    :  t时刻后，追踪星在目标星VVLH坐标系的位置和速度 (km,km/s)
%  Phi    :  状态转移矩阵               
%  rvt_phi:  通过状态转移矩阵计算出来的追踪星在目标星VVLH坐标系的位置和速度（用来与rvt做一个对比）
%% 参考文献<New State Transition Matrix for Relative Motion on an Aribitrary Elliptical Orbit>
%% 作者 Yamanaka Koji
global miu Re
miu = 3.986e5;
Re  = 6378.137;
% 计算半长轴
sma =    (Re+Perigee)/(1-ecc);
% 计算半通径
p  =     sma*(1-ecc^2);
% 计算角动量
h  =     sqrt(p*miu);
% 计算归一化的相对位置速度
rho     = 1+ecc*cosd(TA);
r_norm  = rho*delta_r;                                   %式子87
k       = sqrt(h/p^2);
v_norm  = -ecc*sind(TA)*delta_r+(1/(k^2*rho))*delta_v;   %式子87 % 计算不同时刻的真近地点角
tanf=tand(TA/2);
ee=sqrt((1+ecc)/(1-ecc));
tanE=tanf/ee;
% 求偏近地点角
if TA<=180E = atand(tanE)*2;
elseE=  atand(tanE)*2+360;
end
% 求平近地点角
M = rad2deg(deg2rad(E)-ecc*sind(E));
% 求平均角速度
n = sqrt(miu/sma^3);
% 平近地点角
M_all1=M+rad2deg(n*t);
if M_all1>360int=floor(M_all1/360);M_all=M_all1-int*360;
elseM_all=M_all1;
end% 利用开普勒方程求解每个时刻的偏近地点角,真近地点角
MM=deg2rad(M_all);
E_rad=Kepler_function(ecc,MM);
tanf2=sqrt((1+ecc)/(1-ecc))*tan(E_rad/2);
if E_rad<pi && E_rad>=0f=rad2deg(atan(tanf2)*2);f_all=f;
elseif E_rad>=pif=rad2deg(atan(tanf2)*2)+360;f_all=f;
end% 计算X-Z矩阵
s0            = rho*sind(TA); c0= rho*cosd(TA);
Phi0_inv      =  zeros(4,4);
Phi0_inv(1,1) =  1-ecc^2;
Phi0_inv(1,2) =  3*ecc*(s0/rho)*(1+1/rho);
Phi0_inv(1,3) =  -ecc*s0*(1+1/rho);
Phi0_inv(1,4) =  -ecc*c0+2;
Phi0_inv(2,2) =  -3*(s0/rho)*(1+ecc^2/rho);
Phi0_inv(2,3) =  s0*(1+1/rho);
Phi0_inv(2,4) =  c0-2*ecc;
Phi0_inv(3,2) =  -3*(c0/rho+ecc);
Phi0_inv(3,3) =  c0*(1+1/rho)+ecc;
Phi0_inv(3,4) =  -s0;
Phi0_inv(4,2) =  3*rho+ecc^2-1;
Phi0_inv(4,3) =  -rho^2;
Phi0_inv(4,4) =  ecc*s0;
Phi0_inv1     =  Phi0_inv.*(1/(1-ecc^2));% 根据f_all 计算每个时刻对应的转移矩阵 X-Z
xz0     =   [r_norm(1);r_norm(3);v_norm(1);v_norm(3)];
y0      =   [r_norm(2);v_norm(2)];
% 计算转移初始值
hatxz0  =   Phi0_inv1*xz0;
% 转移矩阵
% 已知 t 时刻的真近地点角
theta   =    f_all;
% 计算矩阵的参数
rho1    =    1+ecc*cosd(theta);
s1      =    rho1*sind(theta);
c1      =    rho1*cosd(theta);
ds1     =    cosd(theta)+ecc*cosd(2*theta);
dc1     =    -(sind(theta)+ecc*sind(2*theta));
J1      =    k^2*t;
%  转移矩阵的参数
Phi_theta       =  zeros(4);
Phi_theta(1,1)  =  1;
Phi_theta(1,2)  =  -c1*(1+1/rho1);
Phi_theta(1,3)  =  s1*(1+1/rho1);
Phi_theta(1,4)  =  3*rho1^2*J1;
Phi_theta(2,2)  =  s1;
Phi_theta(2,3)  =  c1;
Phi_theta(2,4)  =  2-3*ecc*s1*J1;
Phi_theta(3,2)  =  2*s1;
Phi_theta(3,3)  =  2*c1-ecc;
Phi_theta(3,4)  =  3*(1-2*ecc*s1*J1);
Phi_theta(4,2)  =  ds1;
Phi_theta(4,3)  =  dc1;
Phi_theta(4,4)  =  -3*ecc*(ds1*J1+s1/rho1^2);
%  利用XZ转移矩阵求出该时刻的位置和速度
hatxz           =   Phi_theta*hatxz0;
xt              =   hatxz(1,1)/rho1;
zt              =   hatxz(2,1)/rho1;
vxt             =   k^2*(hatxz(1,1)*ecc*sind(theta)+hatxz(3,1)*rho1);
vzt             =   k^2*(hatxz(2,1)*ecc*sind(theta)+hatxz(4,1)*rho1);
%  Y转移矩阵的参数
Phi_thetay      =   zeros(2);
Phi_thetay(1,1) =   cosd(theta-TA);
Phi_thetay(1,2) =   sind(theta-TA);
Phi_thetay(2,1) =   -sind(theta-TA);
Phi_thetay(2,2) =    cosd(theta-TA);
haty(1,:)       =    Phi_thetay*y0;
yt              =    haty(1,1)/rho1;
vyt             =    k^2*(haty(1,1)*ecc*sind(theta)+haty(1,2)*rho1);
rvt             =    [xt,yt,zt,vxt,vyt,vzt];
% 求出归一化形式的状态转移矩阵
% 首先X-Z形式的矩阵
Phi_XZ  = Phi_theta*Phi0_inv1;
Phi_Y   = Phi_thetay;
% 归一化的状态转移矩阵
Phi_hat = zeros(6,6);
Phi_hat(1,1) = Phi_XZ(1,1);
Phi_hat(1,3) = Phi_XZ(1,2);
Phi_hat(1,4) = Phi_XZ(1,3);
Phi_hat(1,6) = Phi_XZ(1,4);
Phi_hat(3,1) = Phi_XZ(2,1);
Phi_hat(3,3) = Phi_XZ(2,2);
Phi_hat(3,4) = Phi_XZ(2,3);
Phi_hat(3,6) = Phi_XZ(2,4);
Phi_hat(4,1) = Phi_XZ(3,1);
Phi_hat(4,3) = Phi_XZ(3,2);
Phi_hat(4,4) = Phi_XZ(3,3);
Phi_hat(4,6) = Phi_XZ(3,4);
Phi_hat(6,1) = Phi_XZ(4,1);
Phi_hat(6,3) = Phi_XZ(4,2);
Phi_hat(6,4) = Phi_XZ(4,3);
Phi_hat(6,6) = Phi_XZ(4,4);
% Y
Phi_hat(2,2) = Phi_Y(1,1);
Phi_hat(2,5) = Phi_Y(1,2);
Phi_hat(5,2) = Phi_Y(2,1);
Phi_hat(5,5) = Phi_Y(2,2);
% 求出初始时间的状态转移矩阵
PhiX0=zeros(6,6);
PhiX0(1,1) = rho;
PhiX0(2,2) = rho;
PhiX0(3,3) = rho;
PhiX0(4,1) = -ecc*sind(TA);
PhiX0(5,2) = -ecc*sind(TA);
PhiX0(6,3) = -ecc*sind(TA);
PhiX0(4,4) = 1/(k^2*rho);
PhiX0(5,5) = 1/(k^2*rho);
PhiX0(6,6) = 1/(k^2*rho);
% 求出末端时间的状态转移矩阵
PhiXt = zeros(6,6);
PhiXt(1,1) = 1/rho1;
PhiXt(2,2) = 1/rho1;
PhiXt(3,3) = 1/rho1;
PhiXt(4,1) = k^2*ecc*sind(theta);
PhiXt(5,2) = k^2*ecc*sind(theta);
PhiXt(6,3) = k^2*ecc*sind(theta);
PhiXt(4,4) = k^2*rho1;
PhiXt(5,5) = k^2*rho1;
PhiXt(6,6) = k^2*rho1;
Phi        = PhiXt*Phi_hat*PhiX0;
rvt_phi=Phi*[delta_r;delta_v];
end

2.利用主函数调动子函数的方法来实现功能

clc;clear
%% 本代码旨在验证TH方程的正确性
%% 验证ecc=0.7的案例
delta_r=[0.1;0.01;0.01];
delta_v=[0.0001;0.0001;0.0001];
t=0:60:1200*60;
vr=zeros(length(t),6);
vrt_phi=zeros(length(t),6);
ecc=0.7;Perigee=500;
for j=1:length(t)[vrt,Phi,vrt_phi1]=TH_solver(0.7,500,45,delta_r,delta_v,t(j));vr(j,:)=vrt;vrt_phi(j,:)=vrt_phi1';
end
figure(1)
load STKVVLh2.mat
plot(Tar_x(1:1200),Tar_z(1:1200),'b--');
axis([-20 5 -5 4])
set(gca,'XDir','reverse');
set(gca,'YDir','reverse');
set(gca,'FontName','Times New Roman')
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Z axis(km)','FontName','Times New Roman')
title(['e=',num2str(ecc),' Perigee=',num2str(Perigee),'km'],'FontName','Times New Roman')
grid on
hold on
plot(vr(:,1),vr(:,3),'r-')
plot(vrt_phi(:,1),vrt_phi(:,3),'g--')
legend(['Numercial'],['TH-Numberical'],['TH-State Transition Matrix'],'Location','southeast')
hold off
figure(2)
plot(Tar_x(1:1200),Tar_y(1:1200));
axis([-20 5 -0.8 0.6])
set(gca,'XDir','reverse');
set(gca,'FontName','Times New Roman')
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Y axis(km)','FontName','Times New Roman')
title(['e=',num2str(ecc),' Perigee=',num2str(Perigee),'km'],'FontName','Times New Roman')
grid on
hold on
plot(vr(:,1),vr(:,2),'r-')
plot(vrt_phi(:,1),vrt_phi(:,2),'g--')
legend(['Numercial'],['TH-Numberical'],['TH-State Transition Matrix'],'Location','southeast')
%% 验证ecc=0.1的案例
t=0:60:220*60;
vr=zeros(length(t),6);
vrt_phi=zeros(length(t),6);
ecc=0.1;Perigee=500;
for j=1:length(t)[vrt,Phi]=TH_solver(0.1,500,45,delta_r,delta_v,t(j));vr(j,:)=vrt;vrt_phi(j,:)=vrt_phi1';
end
figure(3)
load STKVVLh.mat
plot(Tar_x(1:220),Tar_z(1:220),'b--');
axis([-3.5 0.5 -0.6 0.3])
set(gca,'XDir','reverse');
set(gca,'YDir','reverse');
set(gca,'FontName','Times New Roman')
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Z axis(km)','FontName','Times New Roman')
title(['e=',num2str(ecc),' Perigee=',num2str(Perigee),'km'],'FontName','Times New Roman')
grid on
hold on
plot(vr(:,1),vr(:,3),'r-')
plot(vrt_phi(:,1),vrt_phi(:,3),'g--')
legend(['Numercial'],['TH-Numberical'],['TH-State Transition Matrix'],'Location','southeast')
hold off
figure(4)
plot(Tar_x(1:220),Tar_y(1:220),'b--');
axis([-3.5 0.5 -0.2 0.15])
set(gca,'XDir','reverse');
set(gca,'FontName','Times New Roman')
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Y axis(km)','FontName','Times New Roman')
title(['e=',num2str(ecc),' Perigee=',num2str(Perigee),'km'],'FontName','Times New Roman')
grid on
hold on
plot(vr(:,1),vr(:,2),'r-')
plot(vrt_phi(:,1),vrt_phi(:,2),'g--')
legend(['Numercial'],['TH-Numberical'],['TH-State Transition Matrix'],'Location','southeast')

其中 STKVVLh,STKVVLh2的数据通过STK计算得到的VVLH坐标系，其数据在作者的数据包里可以免费下载，最后得到四个图

这篇关于TH方程学习（4）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---