本文主要是介绍浅谈线性化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
浅谈线性化
原文:浅谈线性化 - 知乎 (zhihu.com)
All comments and opinions expressed on Zhihu are mine alone and do not necessarily reflect those of my employers, past or present.
本文内容所有内容仅代表本人观点,和Mathworks无关
(这里所说的线性化,包括下面会用到的"Exact Linearization", 都是指基于一阶泰勒展开的线性化近似,而不是基于微分几何的全局线性化或者输出反馈线性化。)
1 为什么要探讨线性化?
很多人看到这个题目,或许第一感觉会是:“为什么要研究线性化?线性化不就是一阶泰勒展开吗?这再简单不过了,用小学数学就好啦!”
在理论上,这一点也没错。比如我们要在原点线性化如下的非线性模型,相信大多数人不假思索的就能告诉我:线性化的结果是 y = u
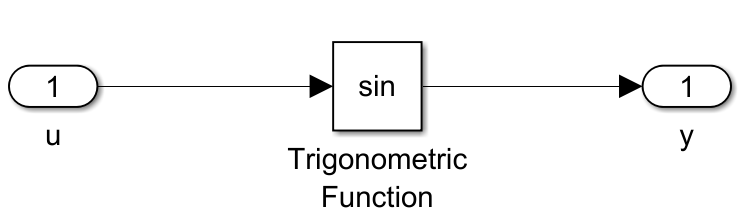
既然如此,我们为什么还要探讨线性化呢? 答案很简单,上面一个例子是理论上的,也就是经过很大程度上简化了的,几乎完美的。那么实际上,工程中需要线性化的问题是什么样的呢?
看看下面的例子,假如有这样一个遥控飞机的模型。工程师现在想把控制器参数优化一下。为此,他需要线性化从飞机控制器的输入到导航控制器的输入之间这个可能含有几千个模块,几万个信号的子系统。很显然,想要解析的泰勒展开这样一个模型,在实际中是相当费时费力的。
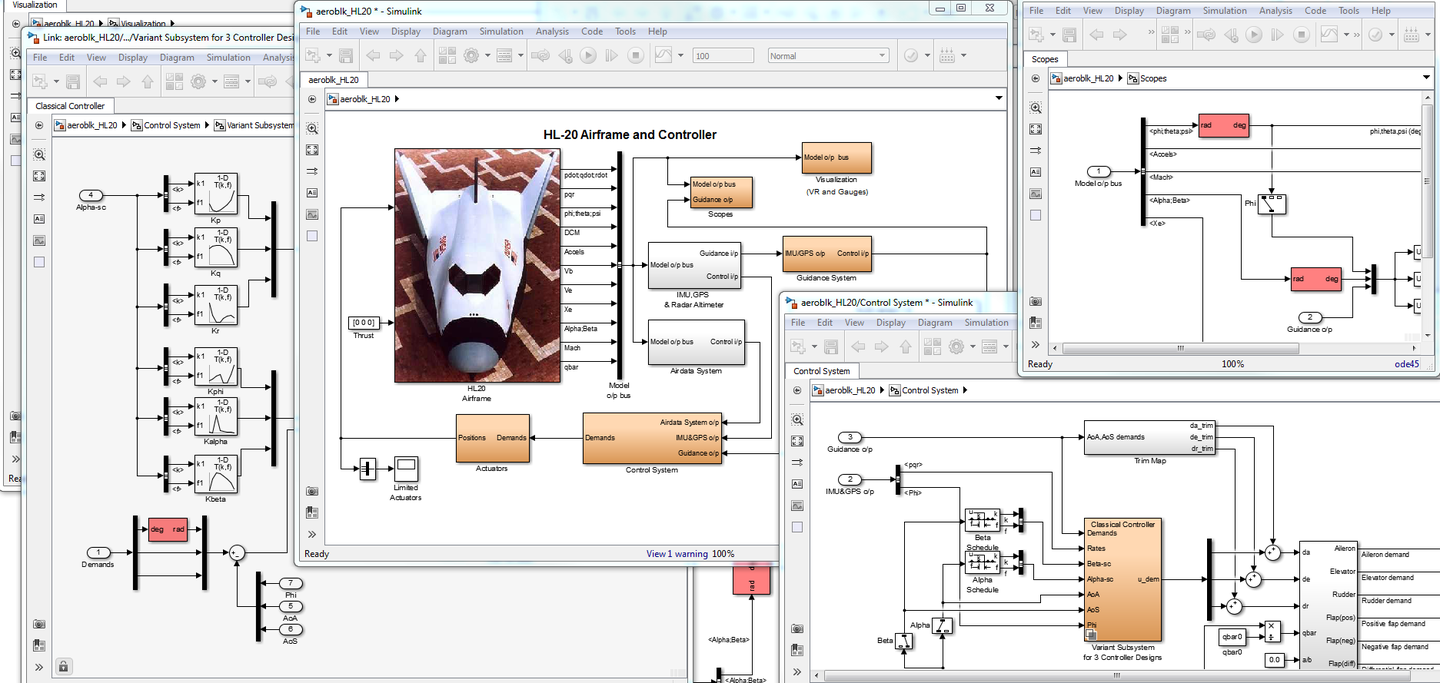
那么,我们来看看难点都在哪吧:
1) 没有非线性方程:
理论上,动态系统总是可以用光滑的ODE来建模。而实际上,在工程应用中,系统往往是用框图来搭建的,比如用Simulink等软件。 用框图来建模有非常多的好处,比如可以方便的模块化,通过观察某个具体的信号值来debug, 还有其他的好处就不一一列举了。但是像这样复杂的框图模型是很难等价的转化成一组非线性方程组的。甚至有些模块,根本就不存在解析表达式。所以,很难对一个非线性方程去求偏导数来获得泰勒一阶展开项。
2) 不光滑:
有些模块或许存在解析数学表达式,但是根本不可导;有些可能存在大量的奇异点;有些甚至导数无从定义,比如enabled subsystem, triggered subsystem等。
3)多重采样时间:
在很多实际模型里面,有些模块是连续的,例如积分器。有些模块是离散的,采样时间可以是0.1秒,可以是10秒,甚至可以是无穷大,比如constant block。那么,最后线性化出来的系统到底应该是连续的,还是离散的?
4) 牵一发而动全局:
假设,在最理想的情况下:我们真的把这个模型对应的非线性方程组表示出来了, 并且最终验证了模型的准确性,然后成功的进行了线性化。可是,第二天模型的作者表示:”我把某几个子系统里的几条信号删掉了,然后把其它几条信号的连接方式重新设计了一下,你再帮我泰勒展开一下吧“。很不幸,这很大程度上意味着我们之前的解析方程组被彻底改变了,所有的工作需要重头在来过。这样的分析方式在实际的工程开发中是很不现实的,因为时间成本太高。
2 数值扰动
既然解析方法不行,那么应该怎么做呢?一个比较传统而且有效的方法是数值扰动。我们还是来看看第一个例子。

用数值扰动的方法,我们可以在输入端输入一个常数,比如说du = 0.1。 然后, 我们测量输出信号,发现 dy = 0.0998, 两者相除,我们得到了一个基于数值线性化的结果
y = 0.998*u
如果用更小的du,事实上我们可以得到更精确的结果。
现在这个方法看起来比解析方法好用了很多。在某种程度上,它的思想其实就是把整个系统当成是一个黑箱,通过输入输出来进行辨识。事实上,对于比较小和比较简单的模型,数值扰动的效果都还是不错的。
那么,它有什么问题呢?看几个例子就能明白了。
2. 1 延时的处理
我们来看看下面这个例子:
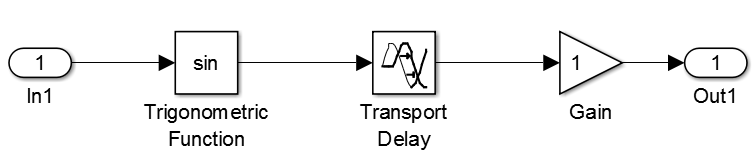
在“黑箱”中,有一个隐藏的很深的延时模块。在这种情况下,我们给这个系统提供扰动输入,然后去测量输出的时候,会发现输出信号过了很久都没有发生变化。由此,我们很有可能会错误的把这个系统线性化成一个 0 增益! 当然了,如果事先能知道其中有一个这样的Delay block,是可以采取一些措施来进行更好的辨识的。但即使如此,自动控制原理告诉我们,在频域上逼近一个Delay Block的一个很好的方式是用Pade Approximation。 但是这种逼近用数值扰动是很难做到的,特别是对于复杂的,含有多个具有不同时间长度的延时环节的系统。
现在,你也许已经可以看出此处存在的一个矛盾: 数值扰动是把整个模型当成一个黑箱,不需要知道黑箱里面的信息。但是我们实际上是知道这个黑箱里所有模块的具体情况的。可是这些信息在数值扰动的过程中没法有效的利用上。
2.2 一些特殊的模块
再看看下面这个例子

假如我们用数值扰动来线性化这个模型,那么我们会遇到两个不同的情况:1)扰动的足够小,我们得到的是一个 0 增益的线性化结果。2)扰动信号大到一定的程度,我们会得到一个线性的关系。
那么,哪个结果是对的呢?答案是:都对,也都不对。这取决于用户的具体问题。如果用户故意用这样一组quantizer, 目的就是想分析在一个很小的范围内此模型的动态。在此情况下那么1)是所期望的。还有一种可能,就是用户本身是不想用Quantizer的,但是在用数字电路实现某个部件的时候,不得已的让一个本来应该是线性增益的关系变成了这样的Quantization的结果。那么在这种情况,2)是用户所期望的。
对于这样一个特殊的模块,我们的确可以通过调整干扰信号的大小来得到不同的结果。但是假设有无数多个类似这样的模块存在于某个模型中,有些模块是属于情况1)的,有些是属于情况2)的,那么整个基于数值扰动的线性化结果就无法如用户所期望的了。
Simulink Control Design工具箱和Block-by-Block方法
Simulink Control Design 工具箱的一大特点就是它提供了Block-by-Block的线性化方法。这个方法有时也叫Exact Linearization (不同于基于微分几何的全局线性化)。简单来讲,在线性化的过程中,每个模块会先被线性化,算出各自的Jacobian矩阵。然后由Simulink Control Design工具箱把这些信息有效的整合在一起(这是一个非常复杂的过程),从而计算出整个模型的线性化结果。
在这个例子中,

线性化通路上有3个模块,他们的Jacobian分别是 cos(0) = 1, n阶的pade approximation的状态空间表达式,和1. 那么对于这个简单的系统而言,整个线性化的结果就是这三个线性系统的级联。
在第二个例子中

用户可以打开Quantizer的窗口,然后
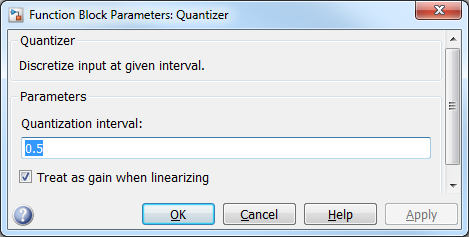
把 Treat as gain when linearizing 的选项打上勾,这样就会使得这个模块被线性化成一个线性增益。
Simulink Control Design工具箱还带有各种高级的功能。例如,对于一些很难线性化的模块,用户可以自己配置此模块的线性化结果,用于整个模型或者子系统的线性化。
更多的内容请参考Simulink Control Design的官方文档:
Simulink Control Design Documentation
这篇关于浅谈线性化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








