本文主要是介绍TH方程学习(3),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、编程实现
根据论文给出的案例,使用TH方程进行数值仿真
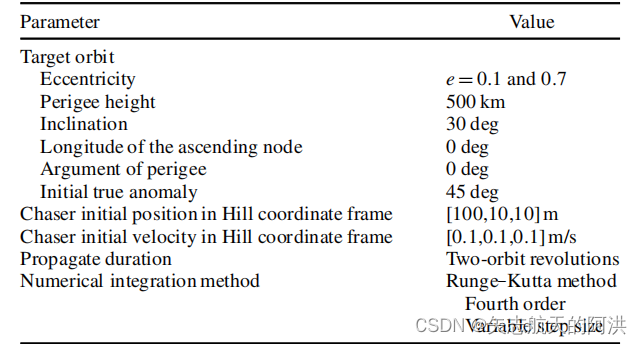
1.初始化条件
%% 参考文献<New State Transition Matrix for Relative Motion on an Aribitrary Elliptical Orbit>
%% 作者 Yamanaka Koji
clc;clear
global miu Re
miu = 3.986e5;
Re = 6378.137;
% step1:初始化条件
ecc = 0.1;
Perigee = 500;
inc = 30;
TA = 45 ;
% 计算半长轴
sma = (Re+Perigee)/(1-ecc);
% 计算半通径
p = sma*(1-ecc^2);
% 计算角动量
h = sqrt(p*miu);
% 计算该近地点时刻的位置大小
r = p/(1+ecc*cosd(TA));
% 计算该时刻的速度
v = sqrt(miu*(2/r-1/sma));
% 计算该时刻的角速度
omega = h/r^2;
rho = 1+ecc*cosd(TA);
k = sqrt(h/p^2);2.求真近地点角
假设迭代时间为13200秒,时间步长取为60s,一共221个数据,首先计算每个时刻的真近地点角,根据给定的初始真近地点角,求出平近地点角,偏近地点角。
t=[0:1:220]*60;
tanf=tand(TA/2);
ee=sqrt((1+ecc)/(1-ecc));
tanE=tanf/ee;
% 求偏近地点角
E = atand(tanE)*2;
% 求平近地点角
M = rad2deg(deg2rad(E)-ecc*sind(E));求出平均角速度
% 求平均角速度
n = sqrt(miu/sma^3);根据初始平近地点角和平均角速度求出,每个时刻对应的平近地点角
% 求出每个时刻的平均角速度
M_all=M+rad2deg(n*t);
for i=1:length(M_all)if M_all(i)>360int=floor(M_all(i)/360);M_all(i)=M_all(i)-int*360;elsecontinueend
end根据开普勒方程,求出偏近地点角,这里采用函数Kepler_function,求出每个时刻对应的偏近地点角和真近地点角
for i=1:length(M_all)MM=deg2rad(M_all(i));E_rad=Kepler_function(ecc,MM);tanf2=sqrt((1+ecc)/(1-ecc))*tan(E_rad/2);if E_rad<pi && E_rad>=0f=rad2deg(atan(tanf2)*2);f_all(i)=f;elseif E_rad>=pif=rad2deg(atan(tanf2)*2)+360;f_all(i)=f;endE_all(i)=rad2deg(E_rad);
endfunction E=Kepler_function(e,M)
% ~~~~~~~~~~~~~~~~~~~~~~~~~~
% 这个函数使用牛顿迭代的方法求解开普勒方程
% 给定偏心率和平近点角
% E-篇近点角(弧度)
% e-偏心率
% M-平近点角(弧度)
% ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
error=1.0e-8;
if M<piE=M+e/2;
elseE=M-e/2;
end
% 迭代要求在所要求的范围内:
ratio=1;
while abs(ratio)>errorratio=(E-e*sin(E)-M)/(1-e*cos(E));E=E-ratio;
end
end求出的每个时刻的三种角与STK计算出来的对比结果
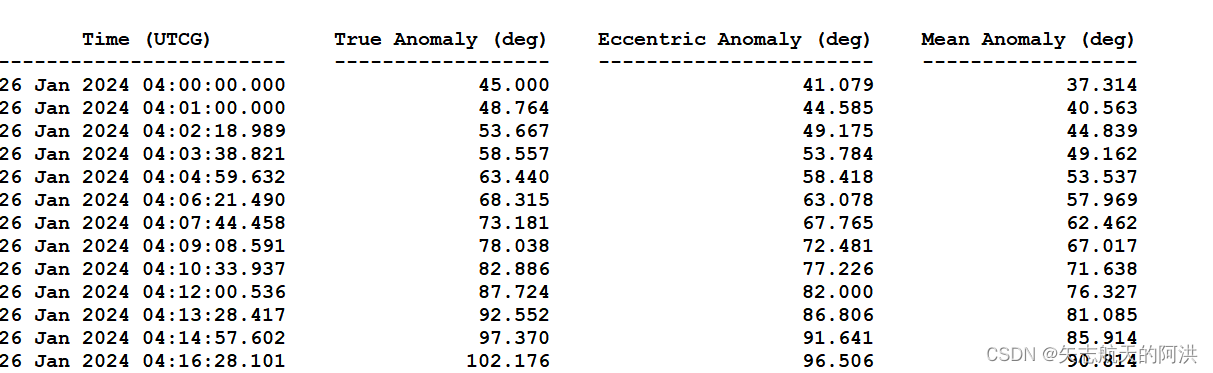
3.代入TH方程
首先求出K值,在目标星的VVLH坐标系,追踪星的位置速度为[0.1km,0.01km,0.01km,0.0001km/s,0.0001km/s,0.0001/s],首先求出XZ轴平面的初始值
r_target = [0;0;-r];
omega_vec= [0;-omega;0];
v_x = miu/h*(1+ecc*cosd(TA)); % 沿着周向的速度
v_z = miu/h*ecc*sind(TA); % 沿着径向的速度
v_target = [v_x;0;v_z]; % 目标星的速度矢量
% 旋转系追踪星相对目标星的位置
delta_r=[0.1;0.01;0.01];
delta_v=[0.0001;0.0001;0.0001];
% 惯性系追踪星的位置
r_chaser=r_target+delta_r;
% 惯性系追踪星的速度
v_chaser=v_target+delta_v+cross(omega_vec,delta_r);% 计算归一化的相对位置速度
rho = 1+ecc*cosd(TA);
delta_r = [0.1;0.01;0.01];
r_norm = rho*delta_r; %式子87
k = sqrt(h/p^2);
v_norm = -ecc*sind(TA)*delta_r+(1/(k^2*rho))*delta_v; %式子87 求出
% 计算X-Z矩阵
s0 = rho*sind(TA); c0= rho*cosd(TA);
Phi0_inv =zeros(4,4);
Phi0_inv(1,1)=1-ecc^2;
Phi0_inv(1,2)=3*ecc*(s0/rho)*(1+1/rho);
Phi0_inv(1,3)=-ecc*s0*(1+1/rho);
Phi0_inv(1,4)=-ecc*c0+2;
Phi0_inv(2,2)=-3*(s0/rho)*(1+ecc^2/rho);
Phi0_inv(2,3)=s0*(1+1/rho);
Phi0_inv(2,4)=c0-2*ecc;
Phi0_inv(3,2)=-3*(c0/rho+ecc);
Phi0_inv(3,3)=c0*(1+1/rho)+ecc;
Phi0_inv(3,4)=-s0;
Phi0_inv(4,2)=3*rho+ecc^2-1;
Phi0_inv(4,3)=-rho^2;
Phi0_inv(4,4)=ecc*s0;
Phi0_inv1=Phi0_inv.*(1/(1-ecc^2));求出初始K值
% 根据f_all 计算每个时刻对应的转移矩阵 X-Z
xz0=[r_norm(1);r_norm(3);v_norm(1);v_norm(3)];
% 计算转移初始值
hatxz0=Phi0_inv1*xz0;4.求出每个时刻的状态转移矩阵,以及在相对位置坐标系的位置
hatxz=zeros(length(t),4);
xz =zeros(length(t),4);
% 转移矩阵
for j=1:length(f_all)% 已知真近地点角theta=f_all(j);% 计算矩阵的参数rho1=1+ecc*cosd(theta);s1=rho1*sind(theta);c1=rho1*cosd(theta);ds1=cosd(theta)+ecc*cosd(2*theta);dc1=-(sind(theta)+ecc*sind(2*theta));J1=k^2*t(j);% 转移矩阵的参数Phi_theta=zeros(4);Phi_theta(1,1)=1;Phi_theta(1,2)=-c1*(1+1/rho1);Phi_theta(1,3)=s1*(1+1/rho1);Phi_theta(1,4)=3*rho1^2*J1;Phi_theta(2,2)=s1;Phi_theta(2,3)=c1;Phi_theta(2,4)=2-3*ecc*s1*J1;Phi_theta(3,2)=2*s1;Phi_theta(3,3)=2*c1-ecc;Phi_theta(3,4)=3*(1-2*ecc*s1*J1);Phi_theta(4,2)=ds1;Phi_theta(4,3)=dc1;Phi_theta(4,4)=-3*ecc*(ds1*J1+s1/rho1^2);% 利用转移矩阵求出该时刻的位置和速度hatxz(j,:)=Phi_theta*hatxz0;xt=hatxz(j,1)/rho1;zt=hatxz(j,2)/rho1;vxt=k^2*(hatxz(j,1)*ecc*sind(theta)+hatxz(j,3)*rho1);vzt=k^2*(hatxz(j,2)*ecc*sind(theta)+hatxz(j,4)*rho1);xz(j,:)=[xt,zt,vxt,vzt];
end接下来求Y轴的变化
y0=[r_norm(2);v_norm(2)];
haty =zeros(length(t),2);
yy =zeros(length(t),2);
for j=1:length(f_all)% 已知真近地点角theta=f_all(j);% 计算矩阵的参数rho1=1+ecc*cosd(theta);s1=rho1*sind(theta);c1=rho1*cosd(theta);ds1=cosd(theta)+ecc*cosd(2*theta);dc1=-(sind(theta)+ecc*sind(2*theta));J1=k^2*t(j);% Y转移矩阵的参数 Phi_thetay=zeros(2);Phi_thetay(1,1)=cosd(theta-TA);Phi_thetay(1,2)=sind(theta-TA);Phi_thetay(2,1)=-sind(theta-TA);Phi_thetay(2,2)=cosd(theta-TA);haty(j,:)=Phi_thetay*y0;yt=haty(j,1)/rho1;vyt=k^2*(haty(j,1)*ecc*sind(theta)+haty(j,2)*rho1);yy(j,:)=[yt,vyt];
end5.结果呈现
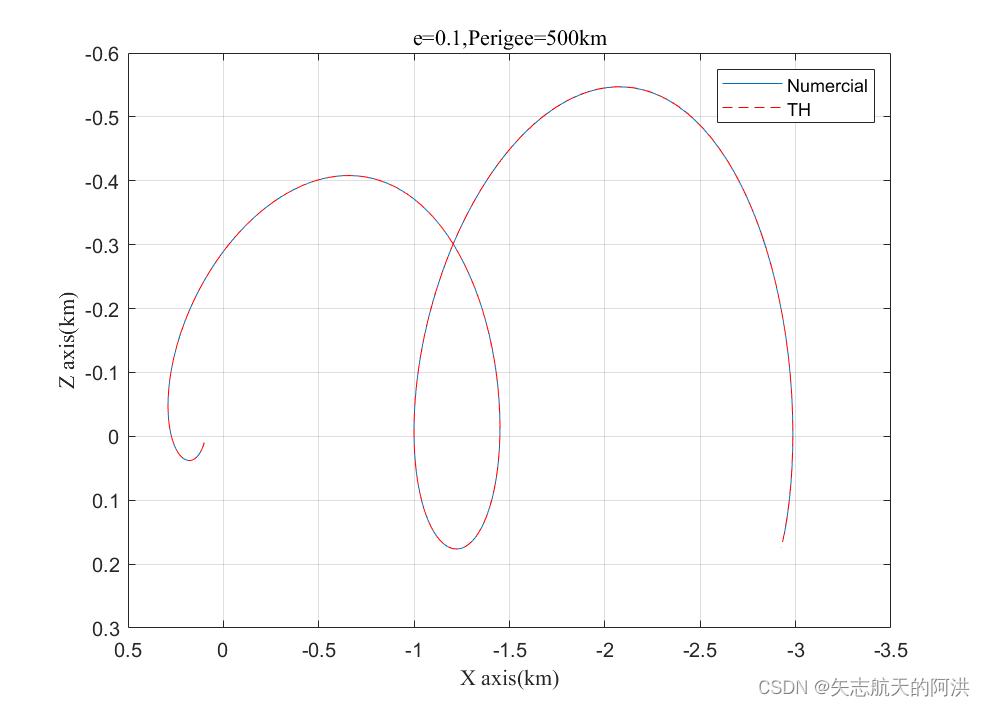
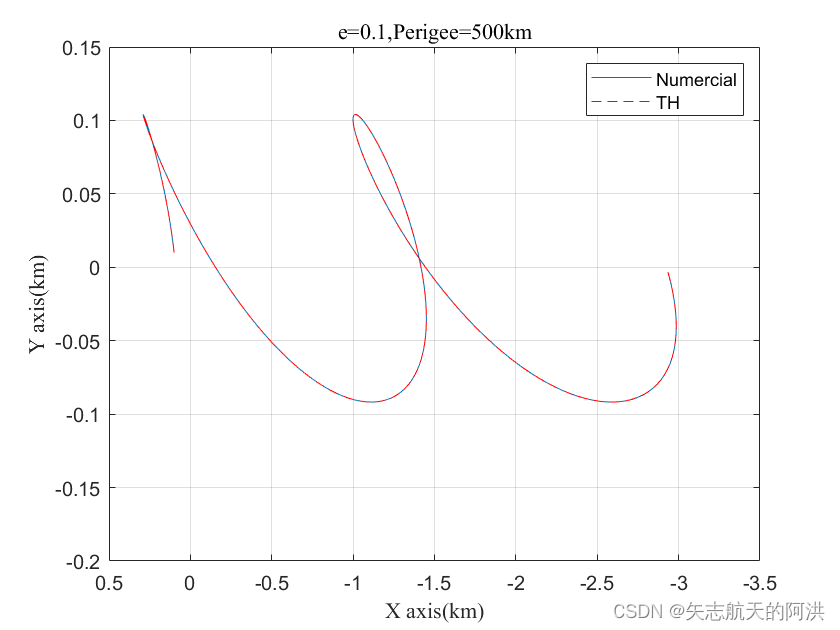
通过对比,发现TH方程求出的相对运动方程与数值计算出来的相对运动方程曲线高度重合,因此TH方程能够解析的描述两个椭圆目标的相对运动方程
这篇关于TH方程学习(3)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








