数字图像处理系列 | 线性滤波（高斯滤波）(3)

本文主要是介绍数字图像处理系列 | 线性滤波（高斯滤波）(3)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

• 我们知道了什么是 线性平移不变系统是在做卷积操作 之后，我们发展出了一些非常简单的 线性滤波， 去增强图片，提取图片特征

1. 卷积如何在离散图片中工作的

• f[i, j]: 离散图片, 是图片中（i，j) 的像素值
  • i: row Number
  • j: Col Number
• M, N 是整张图的大小
• m, n 是卷积核大小
• Convolved by some impulse response h[i,j]
• h[i-m, j-n]: 被称为 ”Mask", “Kernel”, “Filter”
  
  

Vis 原图和mask做卷积时发生了什么

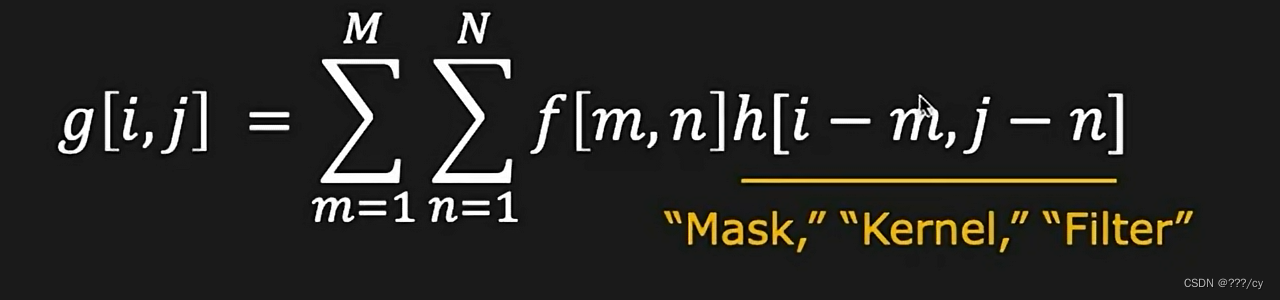
首先，如何得到 (i.j)位置的卷积 g[i,j] 呢？

• h[m, n] 是一个卷积核
  

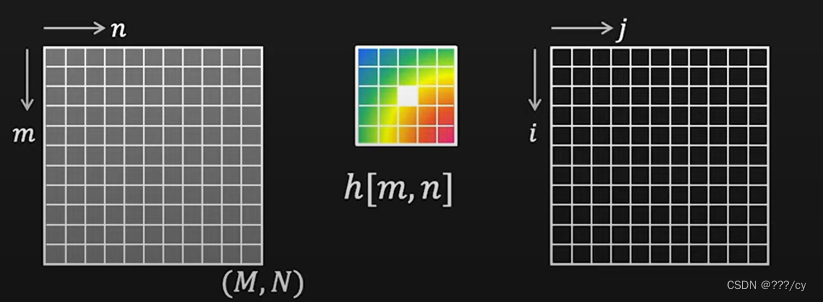
• 反转 h[-m， -n]， 看颜色变了吧

• 这里的h是卷积核哦
  

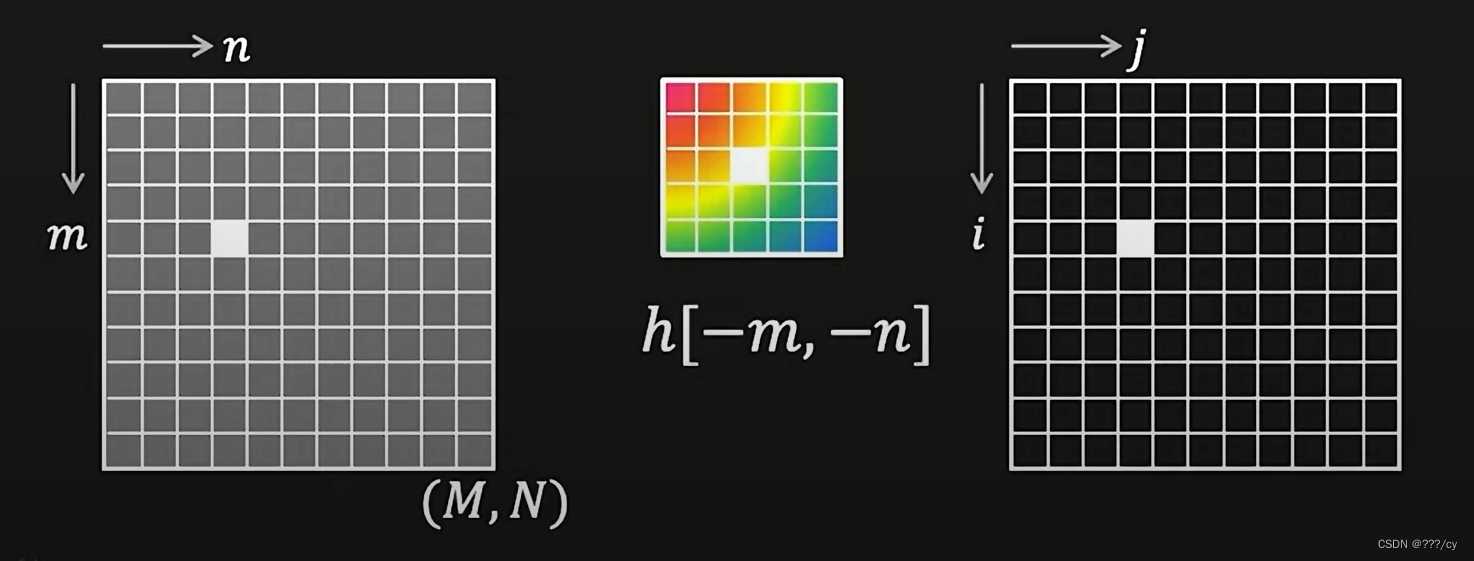
• 然后，把卷积核放在你想得到的坐标那里，这里是**(i, j)的位置**
  

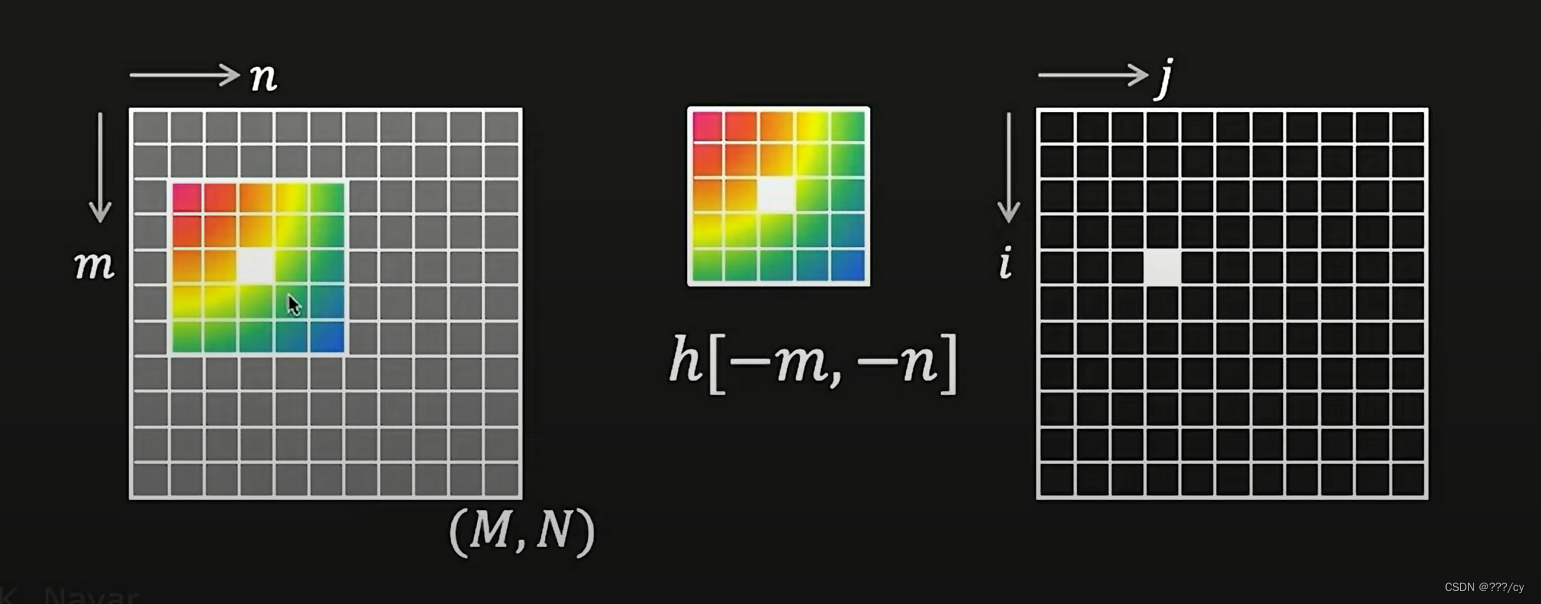
• 做一个卷积相乘，加和，得到右侧的橙色，这就是当前位置的卷积结果。
  

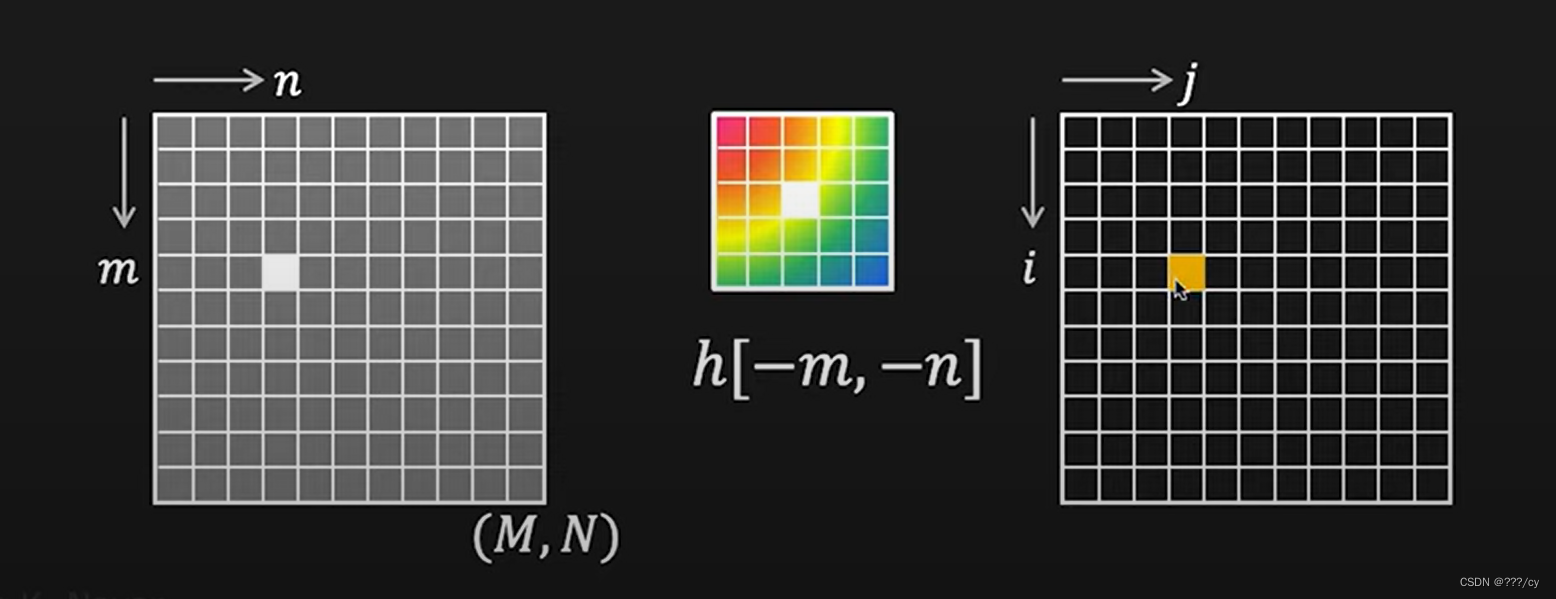
• 你想要得到所有的g[i,j], 你就重复上述动作，1. 旋转你的卷积核，2. slide over entire image

值得注意事情

2. 应用示例：脉冲滤波器 (Impulse Filter)

平移不变性指我们在图像的每个位置都执行相同的操作。线性指这个操作是线性的，也就是我们用每个像素的邻域的线性组合来代替这个像素。

图片平移：Image Shift

• 反转 卷积核，右下角的白色方块 --> 左上角，然后全图经过卷积，原图整体向右，向下移动。
  

图片平均：Averaging

• Box Filter: 汇集了 周围 5x5=25 个像素的值，所以卷积之后，该位置的值会变得非常大，但我们8 bit的图像中，数值范围是从(0, 255)的，所以 超过255的就按255算，反之小于0 的按0 算。
  
• 确保你设计Filter的时候，Filter要做归一化，要不就产生上面的问题了，所有的数字相加都到255 了
• 这样做，图就不会过度曝光了吧，变的平滑了吧
  

平滑滤波 (Smoothing With Box Filter)

• 是不是看起来不太自然，好吧
• 然我们看看下一节，高斯滤波，会让他变的自然起来
  

3. 模糊滤波 (Smoothing With “Fuzzy” Filter)

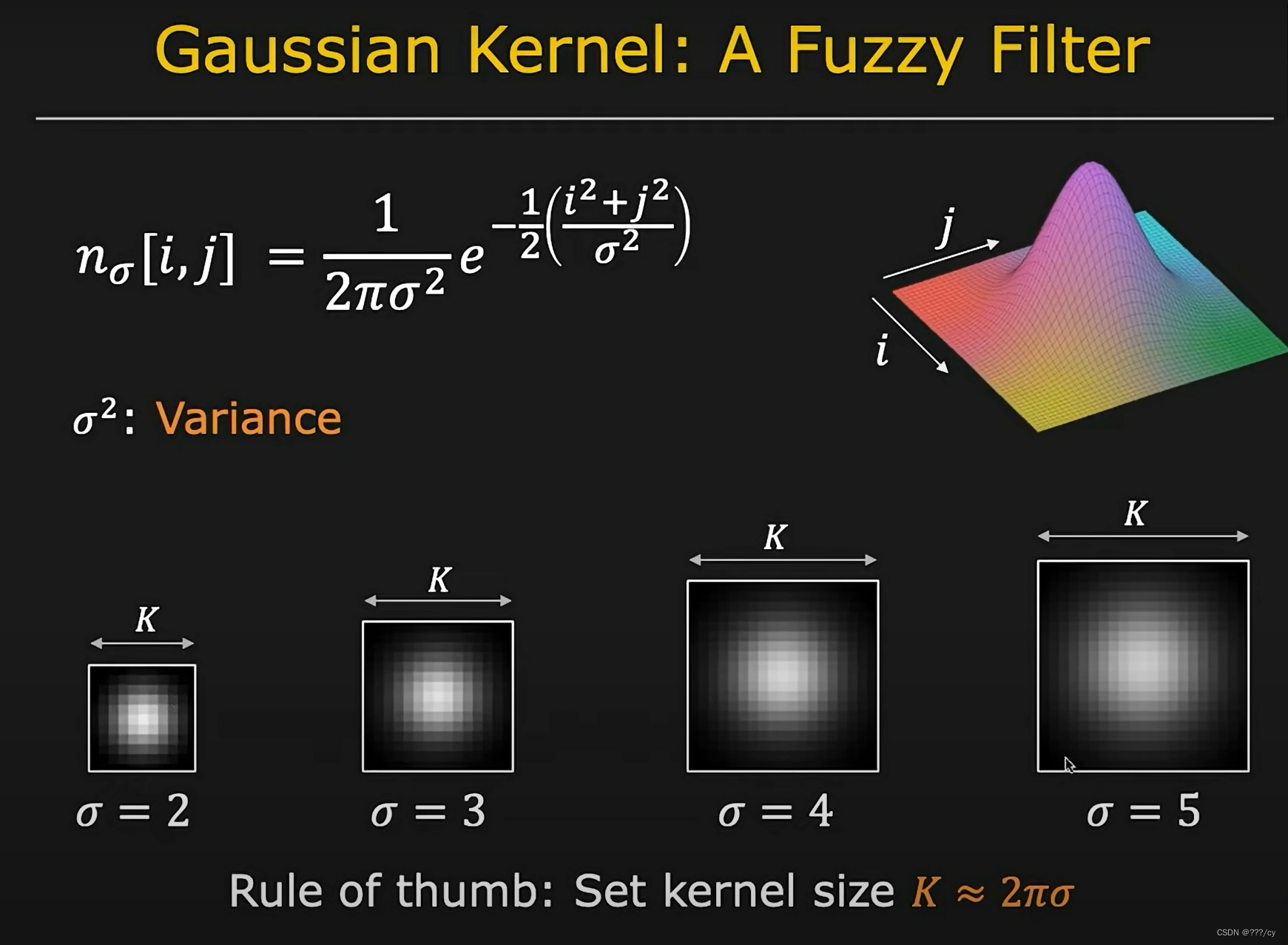
Fuzzy Filter 可以用 高斯卷积核 来表示

• $\sigma 是标准差$
• ${\sigma }^2是方差$
• $\sigma$ 越大，高斯的边界越大
  
• 这里推荐卷积核大小k，因为这能最大化的使用高斯的能量（突出来的部分）
• 我们可以看到σ=5的中央要比，σ=2的中央暗很多，因为k=5的时候像素很多，然后做了归一化就变得很小了
• 推荐的k值为 $$k=2\pi \sigma$$

来看看Guassian Smoothing

• $ \sigma$ 越大越模糊哦
  

为什么高斯滤波 这么受欢迎：因为高斯是可分离的

• 2D 高斯 -> 1D 高斯
• 做1D 高斯计算量会比 2D 小很多
  
  
• 来看看高斯1D, 2D的计算量
  

这篇关于数字图像处理系列 | 线性滤波（高斯滤波）(3)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---