本文主要是介绍【ARM+Codesys案例】树莓派+Codesys软PLC方案在包装行业灌装旋盖机的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
ARM系列支持:全志T3、RK3568、树莓派
机型定义:双工位旋盖机
旋盖机主要适用于不同规格的材质及不同规格的盖、旋(轧)盖。适用螺旋盖、防盗盖、防撞盖、压入盖等。压力可方便调整,根据瓶盖大小设置取盖位。结构紧凑、合理,能方便与其它设备联动成线。机器优点:直线式设计,组成流水线方便美观。
控制流程及要点
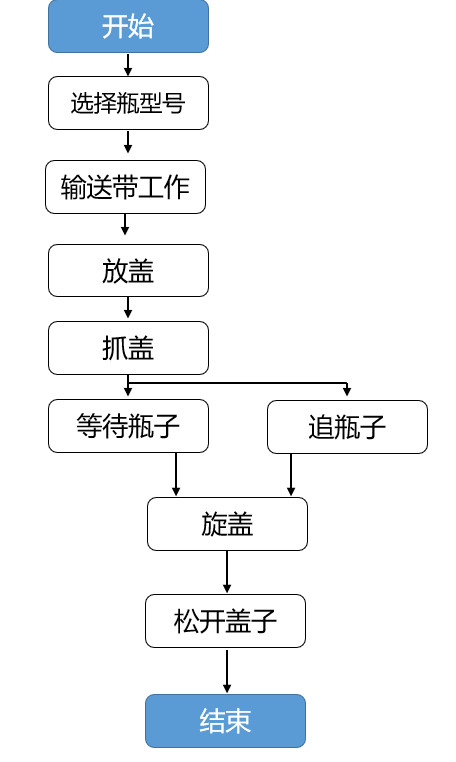
控制要点:
1、设备是流水线工作,同步运动必须到位,采用电子凸轮来实现同速运动,保证旋盖同步。
2、设备是双工位,第一工位(流水线过来第二台)旋盖是光眼检测的单数,第二工位是双数。在程序里面比较通过光眼的瓶数量除以2求余,来比较余数为0或为1的时候触发动作。
3、皮带的速度,和旋盖的力矩是需要调试的,程序里面通过高速计数模块采集通过换算求出传送带频率,传送带周长*传送带频率/1000求出传送带秒速度。
4、两个工位在屏上有对应的位置按钮,方便操作人员定位,可在屏上设置水平等待位置、支架等待位置,方便自动运行时的操作。屏上有清除报警按钮和复位按钮操作。
合信控制方案
控制系统:基于 CODESYS 开发的CTH300系列控制器+ DIT16 + DQT16 + HSC + A4N伺服
主机采用 EtherCAT 总线连接7台高性能伺服驱动A4N。
控制系统配置图

现场图片

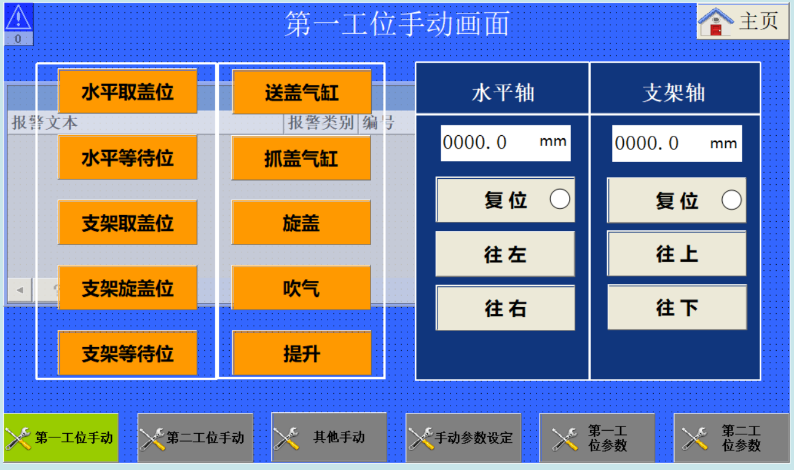

控制系统优势
1 基于 CODESYS 开发的CTH300系列中大型PLC,程序空间和数据空间大,扩展能力强,处理器扫描速度快;
2 CODESYS 集成主流工业总线协议栈,本方案采用高速EtherCAT总线控制伺服系统,接线简洁,控制精度高,速率快,响应实时;
3 通过 CODESYS 软件可以有效地查看跟踪对应的变量的变化曲线,方便调节;
4 CODESYS 集成复杂运动控制功能:支持电子凸轮,可以自定义凸轮曲线,内置丰富的配置选项,可以自由增减推杆数量和触发形式;支持CNC功能,符合DIN 66025的G代码标准,使用多种机构的运动学变换的正逆解算法和路径预处理功能块;支持机器人编程,包含丰富的运动学变换库以支持不同运动学的工业机器人的开发,例如Delta机器人,SCARA机器人以及龙门式机器人等;支持支持虚轴,可以采用虚轴带实轴的形式做项目测试。在旋盖机上使用电子凸轮让工艺过程更好控制。
CODESYS 运动控制优势
CODESYS 将运动控制与逻辑控制合二为一,集成在 IEC61131-3 标准的 CODESYS 编程系统和 CODESYS 实时运行系统中,形成了 CODESYS SoftMotion(CNC)工具包。从单轴运动到复杂 CNC 控制和机器人应用,都可以使用CODESYS SoftMotion(CNC)来编程实现。
与传统的运动控制解决方案相反,CODESYS SoftMotion(CNC)提供了一个直接集成在CODESYS编程环境中的工具包,用以实现运动控制的所有功能。CODESYS SoftMotion(CNC)工具包基于国际标准的IEC 61131-3编程语言,用户可以使用它开发最复杂的运动控制应用程序。
CODESYS SoftMotion 特点
(1)运动控制编程独立于总线和驱动器。
(2)可用于众多标准运动控制器的驱动器,例如CIA DSP 402控制器、步进电机、变频器、虚拟轴等。
(3)可直接在CODESYS编程环境中配置总线和驱动。
(4)提供包含所有运动控制功能块的POU库,可以快速、高效地开发简单运动程序。
(5)支持在集成的编辑器中设计电子凸轮。
(6)支持集成的DIN 66025编辑器(支持G代码)来规划和编辑复杂的动作。
(7)通过使用PLCopen Motion Part 4 和轴组编辑器来开发多轴机器人控制器。
(8)丰富的库函数集,包括几何数据处理(路径预处理),样条曲线计算,CNC刀具位置校正等。
(9)包含丰富的交换库(用于备份和交换数据用),用以支持不同运动学的工业机器人的开发,例如Delta机器人,Scara机器人,Portal机器人以及龙门式机器人等。
(10)支持在线的CAM编辑器和CNC编辑器,机器操作员可以图形化的方式创建和编辑CNC程序。
这篇关于【ARM+Codesys案例】树莓派+Codesys软PLC方案在包装行业灌装旋盖机的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


