看了《概率论与数理统计》上面说了大数定律和中心极限定律的推到。。。。没时间去弄公式推到,现在大概了解,之后用到再去一步步推到。
中心极限定理:
设随机变量X1,X2,......Xn,......独立同分布,并且具有有限的数学期望和方差:E(Xi)=μ,D(Xi)=σ20(k=1,2....),则对任意x,分布函数都符合正太分布。
该定理说明,当n很大时,随机变量
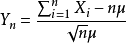
近似地服从标准正态分布N(0,1)。
这里的作用是判断一个模型是否可以符合正太分布,下面课程的房价是一个不固定的因素受到天气、人的心情、道路等。。。因素影响,且这些特征都是独立的,所以可以把房价模型假设为正太分布,同时房价-预测=误差,那么误差也就是满足正太N(0,1)分布了。
两者的区别:
简单来说,大数定律(LLN)和中心极限定理(CLT)的联系与区别在于:
- 共同点:都是用来描述独立同分布(i.i.d)的随机变量的和的渐进表现(asymptotic behavior)
- 区别:首先,它们描述的是在不同的收敛速率(convergence rate)之下的表现,其次LLN前提条件弱一点: 条件强一点:
, CLT成立
多说一句关于收敛速率,假设有 n 个 i.i.d 的随机变量,令它们的和为
1.大数定律(以其中弱大数定律为例)说的是
2.中心极限定理说的是
注意表达式(1)和表达式(2)差了个
所以你就记住这条就不会混乱了,来,跟我念一遍:“差了个
很多人可能有个误区,觉得(2)跟
说的是一回事儿,或者觉得由(3)可以得到(1),但实际上(3)是一个极为不严谨的表述,因为箭头右边理论上是不能带 n 的,带了 n 的话极限就成0了,那就不是在描述一个确定的分布了。
另外还有一个误区,就是觉得应用CLT必须标准化,但是实际上不用除以标准差,(2)本身就是对的。当然除了标准差也不会错,因为根据Slutsky定理,(2)的左边除以一个标准差的一致估计,右边也就相应scale by 标准差,就变成了标准正态分布 N(0, 1)。
3.总结一下
一些自然界的某些事件(满足一定条件),通过大量的练习和测试,结果会出现一个规律的表现。
其中这个规律就是大数定律和中心极值定律:
A.大数定律:取向于某个值(某个规律序列)。
B.中心定律:不仅有趋向的值,而且趋向的快慢和大小都有表现。
参考知乎大神回答:https://www.zhihu.com/question/22913867







