本文主要是介绍闭环设计相关,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
电流环设计,以buck电路为例
(1)主要参数
母线电压600V,电感600uH。开关频率为15000Hz,电流反馈通道的滤波时间常数,取0.000167,具体计算采用mathcad,如下:

图1 mathcad中buck的主参数
上图的中频宽为9的时候设计的PI调节器参数,ts在中频宽为9时,是4.9✖T2,tp是9.0✖T2,此处的4.9和9.0 是按照电子最佳设计,也称rmax准则,查表得出,可见文章末尾的表,由此计算可知峰值时间是1.8ms,上升时间是0.98ms。
电流检测滤波时间和失控时间是高频小惯性环节,可等效为时间常数之和的惯性环节。
Mathcad中if必须要带otherwise!!!
(2)电流环Pi调节器参数计算
0型系统稳态误差低,三型和三型以上的系统很难稳定,如果需要系统又良好的跟随性能,则选择1型 ,如果需要良好的抗扰性能则一般将系统校准为典型2型,二者的传递函数和波特图如下

典型2型系统有俩个转折频率,第一个转折频率受调节器的零点,使得系统的从低频段的-40db变为中频的-20db,
第二个转折频率时受反馈通道的影响,反馈通道的滤波器要滤除开关频率的纹波,时间常数取开关周期的10倍左右,反馈通道为一阶低通滤波器。低通滤波器的极点使得高频段的增益变为-40db。
在中频段,需要-20db穿越0db,又因为电感值和电容值等系统参数均会变化,故需要-20db以一定的宽度穿越,此处设计的中频宽为9。中频宽对控制系统的动态品质起到决定性的作用。

图2-1 K的计算
从上可知,当系统的开关频率确定后,反馈通道的滤波器也基本确定,选择一个中频宽,则调节器的积分时间常数也能确定下来。

注意典型1型是2阶系统,典型2型是3阶系统。
开关模型如下:
调节器:
系统的等效开环传递函数如下
公式2-1
上式T2是失控时间和滤波时间常数的等效。采用电子最佳设计,也称rmax准则,取穿越频率为几何中点,中频宽为9,则可得
公式2-1 中增益为 ,根据图2-1 可得
,可得出
到此pi调节器的设计完成,接下来通过数学放置,物理放置,和实物调试,经行验证。
(3)电流环数学仿真模型
进行数学仿真并验证其上升时间和峰值时间(Psim仿真)

上图中第一行第一个H(s)是PI调节器
其中Ppi为比例系数,T1为积分系数
第一行第二个H(s)是
600是母线电压,0.000033333是平均失控时间,是开关周期的一半。
第一行第三个H(s)是
其中0.000266 电感值
第二行的H(s)是反馈通道滤波器的传递函数,为
15是反馈通道的增益,0.000167是反馈通道的滤波时间常数。
上述中,给定指令为电流指令,则可以将PI调节器看作R(s)传递函数,得出为电压的关系,电压经过开关后,除以感抗,得出的依旧是电流的传递函数,反馈回去依旧是电流的关系式。
仿真结果如下图

仿真中上升时间是0.95ms,峰值时间是1.7ms,与计算得出的上升时间和峰值时间一致,验证正确。
书中所述,均为单位负反馈,所以在仿真时注意响应应该是单位反馈的输出(即观察响应是从反馈的输入,与给定的比较处,来看响应时间)。实际中考虑检测滤波电路一般为一阶延迟惯性环节,所以单位反馈输出等效为滤波电路的输出
(4)电流环物理仿真
物理仿真说的用元器件进行仿真。
如下

上图中的,第一个H(s)是pi调节器,第二个是电流检测滤波环节。图中的K是前馈环节,去除扰动
在实际中,加扰动(如负载突变,属于一种扰动,buck中改变负载,输出电压发生改变,即在环路中有扰动,在实际中如果验证负载突变的扰动,需要对不同扰动类型就行计算),需要看扰动的模型是否与理论模型一致。
在上图中,电感后面需要加一个电阻,此时电阻上的电压就是扰动。电阻的阻值也会影响峰值时间,why加前馈后,影响还是很大??????
仿真波形图如下:

物理仿真与理论计算接近,论证了计算和数学模型的准确性。
(5)电压环调节器设计
双闭环一般电流为内环,电压为外环,在设计电压外环的时候,电流环的闭环传递函数经过降阶近似处理,等效为一阶惯性,如下
0.0006是电流环的穿越频率,
电压检测的时间常数设置为0.0005,分压比为4,则电压检测的传递函数为
电压调节器为Gv(s),此时控制的开环传递函数为
电压检测和电流环的时间常数为高频小时间常数,等效为一个时间常数,等效后的开环传递函数为
将其设计为典型二型环节,则调节器依旧是比例积分调节器
电压环的中频宽设计为9
在mathcad 中计算

可得电压调节器的传递函数为
列出其闭环传递函数,并且反拉普拉斯变化,绘制时域图,如下

则计算可得峰值时间是10ms左右,
至此,电压外环调节器设计完成,进行数学模型仿真和物理模型仿真,以及最后的实物调试,
(5)电压环数学模型仿真
搭建如下,

TFCN1是电压调节器,TFCN2是电流调节器,TFCN3是开关管的模型,TFCN4是电感模型,TFCN5是电容模型,TFCN6是电流检测,TFCN7是,电压检测。
下图是电压外环电流内环的仿真结果。

上图中的峰值时间是11ms,与理论计算相近。
(6)电压环物理模型仿真
搭建电压外环的物理模型。如下图

上图中,电流环有电压前馈,电压环有电流前馈。可理解为扰动,也可理解为在电流环建模时,应该是电感俩端的电压差,积分后才是电感电流,所以,前馈先给指令加上电感右端的电压,等效为电感俩端的电压差。同时,电压环设计时,是电感电流减去负载电流才是电容电流,电容电流在电容上积分才是输出电压。如果仅仅是稳态建模则不需要考虑,在考虑响应时间的时候,就需要考虑。

仿真时间是9.12ms 与理论计算较为接近。
(7)系统总体控制框图
待续。。。
附录
当以开环频率特性相角裕量最大为设计目标时,交越频率设计在几何中点处,为电子最佳设计,也称rmax准则。
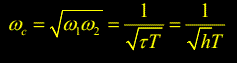
以闭环系统的频率特性为设计目标时,交越频率设计在代数中点处,是Mr.min准则(谐振峰最小)。
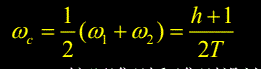
如下表为指标关系。

参考来源电力拖动运动控制系统课件教学配套课件丁学文第2章.pdf全文-大学课件-在线文档
这篇关于闭环设计相关的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






