本文主要是介绍Matlab数字图像处理学习记录【3】——频域处理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
频域处理
- 一.二维离散傅里叶变换
- 二.计算并可视化二维DFT
- 三.频域滤波
- 3.1基本概念
- 3.2 DFT滤波的基本步骤
- 四.从空间滤波器或得频域滤波器
- 五.在频域中直接生成滤波器
- 5.1建立用于实现频域滤波器的网格数组
- 5.2低通滤波器
- 5.3线框图和表面图
- 六.高通滤波器
- 6.1基本高通滤波
- 6.2 高频强调滤波
一.二维离散傅里叶变换
令f(x,y)表示一副M×N的图像,其中x∈0,1,…,M-1和y∈0,1,…,N-1,f的二维离散傅里叶变换可以表示为F(u,v),则可以表示为:
F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F(u,v)= \sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)
我们可以将指数项拓展为正弦项和余弦项的形式,其中变量u和v确定他们的频率。频率系统是由F(u,v)所构成的坐标系。则将该坐标系则可以求傅里叶的逆变换:
F ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 f ( u , v ) e j 2 π ( u x M + v y N ) F(u,v)= \frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}f(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})} F(u,v)=MN1u=0∑M−1v=0∑N−1f(u,v)ej2π(Mux+Nvy)
F(0,0)则被称为傅里叶变换的直流分量,且不难看出F(0,0)是f(x,y)平均值的MN倍
若用R(u,v)和I(u,v)来表示F(u,v)的实部虚部,则有:
∣ F ( u , v ) ∣ = [ R 2 ( u , v ) + I 2 ( u , v ) ] \left| F(u,v) \right|=\sqrt{ \left[ R^2(u,v)+I^2(u,v) \right]} ∣F(u,v)∣=[R2(u,v)+I2(u,v)]
相位角:
ϕ ( u , v ) = a r c t a n [ I ( u , v ) R ( u , v ) ] \phi(u,v) =arctan\left[ \frac{I(u,v)}{R(u,v)}\right] ϕ(u,v)=arctan[R(u,v)I(u,v)]
有相角,则可以表示在极坐标轴里表示:
F ( u , v ) = ∣ F ( u , v ) ∣ e − j ϕ ( u , v ) F(u,v) = \left| F(u,v) \right|e^{-j\phi(u,v)} F(u,v)=∣F(u,v)∣e−jϕ(u,v)
功率谱则是复读的平方:
P ( u , v ) = ∣ F ( u , v ) ∣ 2 P(u,v) = \left| F(u,v) \right|^2 P(u,v)=∣F(u,v)∣2
若f(x,y)是实数,则其傅里叶变换关于原点共轭对称:
F ( u , v ) = F ′ ( − u , − v ) F(u,v) = F'(-u,-v) F(u,v)=F′(−u,−v)
∣ F ( u , v ) ∣ = ∣ F ′ ( − u , − v ) ∣ \left| F(u,v)\right| = \left| F'(-u,-v) \right| ∣F(u,v)∣=∣F′(−u,−v)∣
代入可得DFT是在u,v方向上述周期无穷的,且周期有M和N决定:
F ( u , v ) = F ( u + M , v ) = F ( u , v + N ) = F ( u + M , v + N ) F(u,v) = F(u + M,v) = F(u,v+N) = F(u+M,v+N) F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N)
当然DFT逆变换同理
当我们为了在图像处理里便于观察,我们会通过人为在DFT变换前,将f(x,y)乘以(-1)x+y来将中点移动到(M/2, N/2)
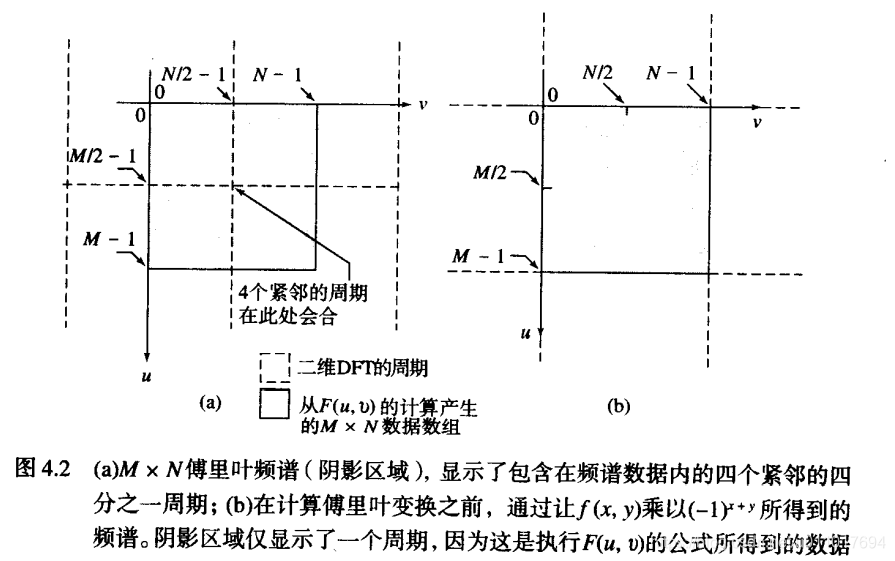
二.计算并可视化二维DFT
使用fft2函数可以快速二维DFT,若想生成固定大小(P,Q)的元素,则添加参数后,会自动填充0
F = fft2(f)
F = fft2(f, P, Q)
频谱则通过abs()函数来求。
f = imread('winbg.jpg');
subplot(2,2,1);
imshow(f);
subplot(2,2,2);
F = fft2(f);
F1 = abs(F);
imshow(F1, []);
subplot(2,2,3);
F2 = fftshift(F);
F3 = ifftshift(F2);
F2 = abs(F2);
imshow(F2, []);
subplot(2,2,4);
F3 = abs(F3);
imshow(F3, []);

函数fftshift()可以将傅里叶变换居中,而iffshift可以重置这种居中。
通过f = real(ifft2(F))可以执行逆变换。
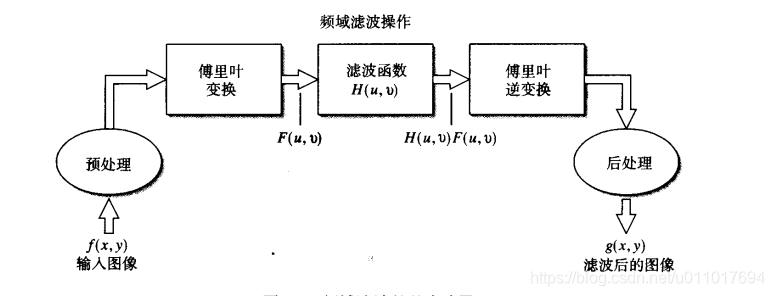
三.频域滤波
3.1基本概念
频域的线性滤波基于的是卷积定理,可以写为:
f ( x , y ) ∗ h ( h , y ) ⇔ H ( u , v ) F ( u , v ) f(x,y)*h(h,y) \Leftrightarrow H(u,v)F(u,v) f(x,y)∗h(h,y)⇔H(u,v)F(u,v)
其中符号*表示表示两个函数的卷积,双箭头两边的表达式组成了傅里叶变换对。表示:两个空间函数的卷积可以通过计算两个傅里叶变换函数的乘积的逆变换得到;相反,两个空间函数的卷积的傅里叶变换恰好等于两个函数的傅里叶变换的乘积。
所以,如果我们要得到图像经过滤波后的图像,则只需要计算H(u,v)F(u,v)的傅里叶逆变换。且需要滤波掩膜h(x,y)是H(x,y)的逆变换。实际上空间卷积会使用较小的掩膜来简化,目的是尽可能或得其频域对应内容的显著特征
为了避免周期函数执行卷积导致相邻周期之间的干扰(折叠误差),所以我们会将图像填充0来避免。一般来说:
假设函数f(x,y)和h(x,y)的大小分别是A×B和C×D,通过对f和g补0,构造两个大小均为P×Q的扩充函数,且P≥A+C-1,Q≥B+D-1
假设我们图片的大小为M × N,此时我们也可以使用P≥2M-1 Q≥2N-1的填充后大小。
所以,写了书上是写了一个自定义大小的函数paddedsize
function PQ = paddedsize(AB, CD, PARAM)
if nargin == 1PQ = 2*AB;
elseif nargin == 2 & ~ischar(CD)PQ = AB + CD - 1;PQ = 2 * ceil(PQ / 2);
elseif nargin == 2m = max(AB);P = 2^nextpow2(2*m);PQ = [P, P];
elseif nargin == 3m = max([AB CD])P = 2^nextpow2(2*m);PQ = [P, P];
elseerror('wrong number of inputs.')
end
然后再通过fft2的自动填充功能,F = fft2(f, PQ(1), PQ(2))即可完成扩充。
使用填充和不使用填充的滤波结果:
对了同时提一下,lpfilter()可以生成一个高斯低通滤波器,有一个参数sigma具体的值,后面再讨论,由于工具箱没内置,代码在这儿:
function [U, V] = dftuv(M, N)
%DFTUV Computes meshgrid frequency matrices.
% [U, V] = DFTUV(M, N) computes meshgrid frequency matrices U and
% V. U and V are useful for computing frequency-domain filter
% functions that can be used with DFTFILT. U and V are both
% M-by-N.% Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.3 $ $Date: 2003/04/16 22:30:34 $% Set up range of variables.
u = 0:(M - 1);
v = 0:(N - 1);% Compute the indices for use in meshgrid.
idx = find(u > M/2);
u(idx) = u(idx) - M;
idy = find(v > N/2);
v(idy) = v(idy) - N;% Compute the meshgrid arrays.
[V, U] = meshgrid(v, u);
function H = lpfilter(type, M, N, D0, n)
%LPFILTER Computes frequency domain lowpass filters.
% H = LPFILTER(TYPE, M, N, D0, n) creates the transfer function of
% a lowpass filter, H, of the specified TYPE and size (M-by-N). To
% view the filter as an image or mesh plot, it should be centered
% using H = fftshift(H).
%
% Valid values for TYPE, D0, and n are:
%
% 'ideal' Ideal lowpass filter with cutoff frequency D0. n need
% not be supplied. D0 must be positive.
%
% 'btw' Butterworth lowpass filter of order n, and cutoff
% D0. The default value for n is 1.0. D0 must be
% positive.
%
% 'gaussian' Gaussian lowpass filter with cutoff (standard
% deviation) D0. n need not be supplied. D0 must be
% positive. % Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.8 $ $Date: 2004/11/04 22:33:16 $% Use function dftuv to set up the meshgrid arrays needed for
% computing the required distances.
[U, V] = dftuv(M, N);% Compute the distances D(U, V).
D = sqrt(U.^2 + V.^2);% Begin filter computations.
switch type
case 'ideal' %理想低通滤波器H = double(D <= D0);
case 'btw' %巴特沃兹低通滤波器if nargin == 4n = 1; endH = 1./(1 + (D./D0).^(2*n));
case 'gaussian' %高斯低通滤波器H = exp(-(D.^2)./(2*(D0^2)));
otherwiseerror('Unknown filter type.')
end
f = imread('winbg.jpg');
[M N] = size(f);
F = fft2(f);
sig = 10;
H = lpfilter('gaussian', M, N, sig);
G = H.*F;
g = real(ifft2(G));
PQ = paddedsize([M N]);
Fp = fft2(f, PQ(1), PQ(2));
Hp = lpfilter('gaussian', PQ(1), PQ(2), 2*sig);
Gp = Hp.*Fp;
gp = real(ifft2(Gp));
gpc = gp(1:M, 1:N);
subplot(2,2,1);
imshow(f);
subplot(2,2,2);
imshow(g, []);
subplot(2,2,3);
imshow(gp, []);
subplot(2,2,4);
imshow(gpc, []);emm图2 4的区别好像不明显

3.2 DFT滤波的基本步骤
总结一下,过程应该分为以下几点:
- 进行缩放填充,比如用刚才写的
paddedsize - 使用填充后的大小,进行傅里叶变换,比如
F=fft2 - 生成一个同样大小滤波函数H,而且该滤波函数并不能居中,否则得转换回去
H = fftshift - 相乘
G=H.*F - 再获得逆变换的实部:
g=real(ifft2(G)) - 最终再缩放大小,比如
gpc = gp(1:M, 1:N);
四.从空间滤波器或得频域滤波器
有文献指出,在滤波器较小的时候,空间滤波器比频域滤波更有效。所以这里会给出从空间滤波器转向频域滤波器的算法。假设h是空间滤波器h,则频域滤波器H的函数可用H = freqz2(h, R, C)
五.在频域中直接生成滤波器
5.1建立用于实现频域滤波器的网格数组
通过自定义的dftuv函数,计算每个像素点距中心点的距离,当然,因为周期性的缘故,所以只用计算1/M和1/N得到,剩下的3/4可以通过周期性复制得到,所以一个巧妙的算法:
function [U, V] = dftuv(M, N)
%DFTUV Computes meshgrid frequency matrices.
% [U, V] = DFTUV(M, N) computes meshgrid frequency matrices U and
% V. U and V are useful for computing frequency-domain filter
% functions that can be used with DFTFILT. U and V are both
% M-by-N.% Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.3 $ $Date: 2003/04/16 22:30:34 $% Set up range of variables.
u = 0:(M - 1);
v = 0:(N - 1);% Compute the indices for use in meshgrid.
idx = find(u > M/2);
u(idx) = u(idx) - M;
idy = find(v > N/2);
v(idy) = v(idy) - N;% Compute the meshgrid arrays.
[V, U] = meshgrid(v, u);
5.2低通滤波器
一个理想的理想的滤波器(ILPF)有的传递函数,其中D0是阈值,为非负数:
H ( u , v ) = { 1 D ( u , v ) ≤ D 0 0 D ( u , v ) > D 0 H(u,v)=\begin{cases} 1 & D(u,v)\leq D_0 \\ 0&D(u,v) >D_0 \end{cases} H(u,v)={10D(u,v)≤D0D(u,v)>D0
D(u,v)为点(u,v)到滤波器中心距离。D(u,v)=D0的轨迹是一个圆。
若H乘以一幅图像的傅里叶变换,则滤波器切断了圆外所有的分量,所以仅保留了圆上和圆内的点。
而n巴特沃兹低通滤波器(BLPF)的传递函数:
H ( u , v ) = 1 1 + [ D ( u , v ) / D 0 ] 2 n H(u,v) = \frac{1}{1+[D(u,v)/D_0]^{2n}} H(u,v)=1+[D(u,v)/D0]2n1
它与理想低通滤波器的不同是,传递函数在D0处是连续的,在D0这个截止频率时,刚好会降低为其最大值的某个给定的比例。比如上式则为50%
而高斯低通滤波器(GLPF)传递函数为:
H ( u , v ) = = e − D 2 ( u , v ) / 2 σ 2 H(u,v) = = e^{-D^2(u,v)/2\sigma^2} H(u,v)==e−D2(u,v)/2σ2
其中σ是标准差,令\sigma=D0则有:
H ( u , v ) = = e − D 2 ( u , v ) / 2 D 0 2 H(u,v) = = e^{-D^2(u,v)/2D^2_0} H(u,v)==e−D2(u,v)/2D02
当D(u,v)=D0时,最大值降为0.607
然后就是写一个函数,统一这几个滤波器:
function H = lpfilter(type, M, N, D0, n)
%LPFILTER Computes frequency domain lowpass filters.
% H = LPFILTER(TYPE, M, N, D0, n) creates the transfer function of
% a lowpass filter, H, of the specified TYPE and size (M-by-N). To
% view the filter as an image or mesh plot, it should be centered
% using H = fftshift(H).
%
% Valid values for TYPE, D0, and n are:
%
% 'ideal' Ideal lowpass filter with cutoff frequency D0. n need
% not be supplied. D0 must be positive.
%
% 'btw' Butterworth lowpass filter of order n, and cutoff
% D0. The default value for n is 1.0. D0 must be
% positive.
%
% 'gaussian' Gaussian lowpass filter with cutoff (standard
% deviation) D0. n need not be supplied. D0 must be
% positive. % Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.8 $ $Date: 2004/11/04 22:33:16 $% Use function dftuv to set up the meshgrid arrays needed for
% computing the required distances.
[U, V] = dftuv(M, N);% Compute the distances D(U, V).
D = sqrt(U.^2 + V.^2);% Begin filter computations.
switch type
case 'ideal' %理想低通滤波器H = double(D <= D0);
case 'btw' %巴特沃兹低通滤波器if nargin == 4n = 1; endH = 1./(1 + (D./D0).^(2*n));
case 'gaussian' %高斯低通滤波器H = exp(-(D.^2)./(2*(D0^2)));
otherwiseerror('Unknown filter type.')
end
5.3线框图和表面图
给一个二维函数H,然后使用mesh(H)即可画出线框图。当然,若H的大小很大,图可能不好看,则可以减少绘制的点:
mesh(H(1:k:end,1:k:end))
当然,还有彩色线colomap([R G B])
然后观测点的位置则通过view(az, el)实现.
[AZ,EL] = view则可以返回现在的角。
view(3)则可以观测我们的图。比如
H = fftshift(lpfilter('gaussian', 500, 500, 50));
mesh(H(1:10:500, 1:10:500));
axis([0 50 0 50 0 1]);
view(-25, 30);

我们换个角度试试?
view(0,20)

六.高通滤波器
6.1基本高通滤波
有了低通,高通就很简单了啊,高通=1-低通
所以写一个hpfilter函数
function H = hpfilter(type, M, N, D0, n)
if nargin == 4n = 1;
end
Hlp = lpfilter(type, M, N, D0, n);
H = 1 -Hlp
end
看看各个滤波器的效果:
subplot(2,3,1);
H1 = fftshift(hpfilter('ideal', 500, 500, 50));
mesh(H1(1:10:500, 1:10:500));
subplot(2,3,4);
imshow(H1, []);
subplot(2,3,2);
H1 = fftshift(hpfilter('btw', 500, 500, 50));
mesh(H1(1:10:500, 1:10:500));
subplot(2,3,5);
imshow(H1, []);
subplot(2,3,3);
H1 = fftshift(hpfilter('gaussian', 500, 500, 50));
mesh(H1(1:10:500, 1:10:500));
subplot(2,3,6);
imshow(H1, []);

6.2 高频强调滤波
我们可以整体把图片调亮,并且给高通滤波器的传递函数,乘以一个值,让它高通通过的部分更高:
H h f e ( u , v ) = a + b H h p ( u , v ) H_{hfe}(u,v) = a + bH_{hp}(u,v) Hhfe(u,v)=a+bHhp(u,v)
比如当a=0.5,b=2时,书中给出了一组和直方图均衡的对比图:

这篇关于Matlab数字图像处理学习记录【3】——频域处理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



