洛谷P3574 [POI2014] FAR-FarmCraft（树形dp）

本文主要是介绍洛谷P3574 [POI2014] FAR-FarmCraft（树形dp），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

$洛谷P3574[POI2014]FAR-FarmCraft（树形dp）$

题目链接：P3574 [POI2014] FAR-FarmCraft - 洛谷

题意

给出$n$个节点、$n-1$条边的一棵无根树；经过每条边所用时间都为$1$。然后每个节点都有点权$b[i]$。

题目故事：管理员从自己家（一号节点）出发，然后将一批电脑分发给每个节点的居民，每个居民得到电脑后会立即开始下载游戏，下载游戏的时间为点权$b[i]$。

管理员每次经过某节点就相当于直接分发给居民。

管理员的车恰好能够走每条路两遍。

要求计算出管理员从开始配送到所有居民都能玩上游戏所用最少时间。

题目说明

给一棵树，走过每条边需要花费一个时间，安装软件又需要花费一个时间，需要遍历整棵树并回到起点，想让所有点中到达时间+安装时间的最大值最小，问这个值是多少？

思路

跟据题目要求，显然能够知道，题目要求求出所有居民中最后玩上游戏的居民所用时间，并且要求这个时间最小。

跟据题目说明，我们可以想到：对于同一个节点的子节点，大致的贪心思路是先遍历点权最大的节点。

但是可能会出现一种情况（画的比较丑陋，多多见谅）：

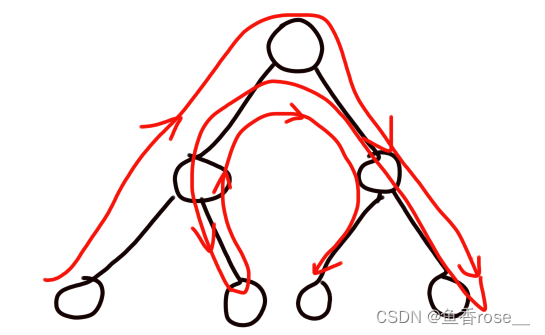
但是我们可以注意到题目有限制条件**“管理员的车恰好能够走每条路两遍”**，那么我们就不用考虑这种情况了。

一般地，我们用$f[i]$表示节点$i$这棵子树中的最大值，$dep[i]$表示从节点$i$出发遍历其子树并返回所用的总时间，$b[i]$表示点权。

容易发现，这道题属于树形dp中的选择节点型，只不过需要判断的是选择子节点的先后顺序。

那么对应的状态转移方程即为：
$$f[x]=\max (f[x],dep[x]+\max (f[i],f[j]+dep[i]+2)+1)$$
其中$x$为当前节点，$i,j$表示它的其中两个子节点。需要解释一下：

• 方程中的+2是因为从一个子节点到另一个子节点的两段路。
• 方程中的+1是因为从$x$节点到子节点的一段路。

但是该这样进行状态转移，我们需要对子节点相互比较，其时间复杂度为$O(n^2)$，会超时。

我们考虑优化状态转移方程：

• 如果先$i$后$j$：$\max (f[i],f[j]+dep[i]+2)$

• 如果先$j$后$i$：$\max (f[j],f[i]+dep[j]+2)$

• 因为$f[i]<f[i]+dep[j]+2$且$f[j]<f[j]+dep[i]+2$

• 原式可化为：$\max (f[j]+dep[i]+2,f[i]+dep[j]+2)$

• 即为：$f[i]-dep[i]<f[j]-dep[j]$（当选$j$时成立）

因此在判断选取子节点时，可以先对子节点按照上述不等式排序，即为选取子节点的先后顺序。

最后需要注意的是，dfs过程中我们并没有判断根节点的时间，需要输出时进行判断取$max$。

标程

#include<bits/stdc++.h>using namespace std;#define IOS ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
#define int long long 
#define ULL unsigned long long 
#define PII pair<int, int>
#define lowbit(x) (x & -x)
#define Mid ((l + r) >> 1)
#define ALL(x) x.begin(), x.end()
#define endl '\n'
#define fi first 
#define se secondconst int INF = 0x7fffffff;
const int Mod = 1e9 + 7;
const int N = 5e5 + 10;int n;
vector<int> a[N];
int b[N], dep[N], f[N];void dfs(int x, int y) {if(x != 1) f[x] = b[x];for(auto i : a[x]) {if(i == y) continue;dfs(i, x);}sort(ALL(a[x]), [](int n1, int n2) {return dep[n1] - f[n1] < dep[n2] - f[n2];});for(auto i : a[x]) {if(i == y) continue;f[x] = max(f[x], f[i] + dep[x] + 1);dep[x] += dep[i] + 2;}
}void Solved() {cin >> n;for(int i = 1; i <= n; i ++ ) {cin >> b[i];}for(int i = 1; i < n; i ++ ) {int x, y; cin >> x >> y;a[x].push_back(y); a[y].push_back(x);}dfs(1, 0);cout << max(f[1], dep[1] + b[1]) << endl;
}signed main(void) {IOSint ALL = 1; // cin >> ALL;while(ALL -- ) Solved();// cout << fixed;//强制以小数形式显示// cout << setprecision(N); //保留n位小数return 0;
}

这篇关于洛谷P3574 [POI2014] FAR-FarmCraft（树形dp）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---