本文主要是介绍用队列实现栈,用栈实现队列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
有两个地方会讨论到栈,一个是程序运行的栈空间,一个是数据结构中的栈,本文中讨论的是后者。
栈是一个先入后出,后入先出的数据结构,只能操作栈顶。栈有两个操作,push 和 pop,push 是向将数据压栈,pop 是将数据出栈。栈还有一个操作 top,这个操作可以查看栈顶的元素,不会出栈。
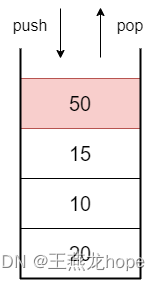
队列是一种先入先出,后入后出的数据结构。

1 用队列实现栈
leetcode 链接:
用队列实现栈
用队列实现栈,队列先入先出以及栈先入后出的语义不能改变。关键是怎么在压栈的时候,将数据放到队列头,这就需要两个队列进行配合。
两个队列配合的方式有两种,这两种方式均可以解答这个问题:
(1)入栈的时候进行元素移动
① 两个队列,始终保持一个队列是空的,假设是队列 A,压栈的时候,将元素放入这个队列。这样最后入队的放到了队列头,所以下次出栈的时候就是第一个出队的。满足先进后出,后进先出的要求,也就是栈的语义。
② 然后将另一个队列(假设是队列 B)里边的元素都移动到这个队列中。
这样,元素都移动到了队列 A 中,队列 B 成为了空队列。下一个元素入队的时候,将元素入队到队列 B,将元素 A 中的元素移动到 B 中。以此类推。
每个元素入队的时候都做这个操作。
第一个元素 10:入队 A,B 中没有元素不需要操作

第二个元素 20:入队 B,A 中的 10 移动到 B
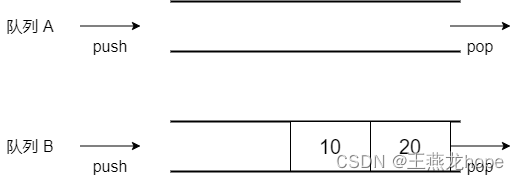
第 3 个元素 30: 入队 A,B 中元素移动到 A

(2)出栈的时候进行元素移动
① 压栈的时候将元素入队到有元素的这个队列里边
② 出栈的时候将元素移动到另一个队列中,同时进行判断,当队列剩余 1 个元素的时候,这个元素就是出栈的元素,不用移动到另一个队列中了。
方法 1 的主要逻辑在 push() 函数中实现;方法 2 的主要逻辑在 top() 和 pop() 函数中都要实现。
两个方法都可以通过两个队列来实现,也可以通过一个队列也是可以实现的。
1.1 入队时处理,双队列
class MyStack {
public:MyStack() {}void push(int x) {if (q_master_.empty()) {q_master_.push(x);while (!q_slave_.empty()) {q_master_.push(q_slave_.front());q_slave_.pop();}} else {q_slave_.push(x);while (!q_master_.empty()) {q_slave_.push(q_master_.front());q_master_.pop();}}}int pop() {if (!q_master_.empty()) {int data = q_master_.front();q_master_.pop();return data;} else {int data = q_slave_.front();q_slave_.pop();return data;}}int top() {if (!q_master_.empty()) {return q_master_.front();} else {return q_slave_.front();}}bool empty() {return q_master_.empty() && q_slave_.empty();}private:std::queue<int> q_master_;std::queue<int> q_slave_;
};1.2 入队时操作,单队列
关键是 push() 函数中的操作,将元素入队之后,然后将新元素之外的元素出队,再重新入队。这样保证了新入队的元素移动到了队列头的位置,下次出栈的时候直接出队就可以。
class MyStack {
public:MyStack() {}void push(int x) {q_.push(x);int size = q_.size();for (int i = 0; i < size - 1; i++) {q_.push(q_.front());q_.pop();}}int pop() {int data = q_.front();q_.pop();return data;}int top() {return q_.front();}bool empty() {return q_.empty();}private:std::queue<int> q_;
};1.3 出队时操作,双队列
class MyStack {
public:MyStack() {}void push(int x) {if (!q_master_.empty()) {q_master_.push(x);} else {q_slave_.push(x);}}int pop() {if (!q_master_.empty()) {int size = q_master_.size();for (int i = 0; i < size - 1; i++) {q_slave_.push(q_master_.front());q_master_.pop();}int data = q_master_.front();q_master_.pop();return data;} else {int size = q_slave_.size();for (int i = 0; i < size - 1; i++) {q_master_.push(q_slave_.front());q_slave_.pop();}int data = q_slave_.front();q_slave_.pop();return data;}}int top() {if (!q_master_.empty()) {int size = q_master_.size();for (int i = 0; i < size - 1; i++) {q_slave_.push(q_master_.front());q_master_.pop();}int data = q_master_.front();q_master_.pop();q_slave_.push(data);return data;} else {int size = q_slave_.size();for (int i = 0; i < size - 1; i++) {q_master_.push(q_slave_.front());q_slave_.pop();}int data = q_slave_.front();q_slave_.pop();q_master_.push(data);return data;}}bool empty() {return q_master_.empty() && q_slave_.empty();}private:std::queue<int> q_master_;std::queue<int> q_slave_;
};1.4 出队时操作,单队列
class MyStack {
public:MyStack() {}void push(int x) {q_.push(x);}int pop() {int size = q_.size();for (int i = 0; i < size - 1; i++) {q_.push(q_.front());q_.pop();}int data = q_.front();q_.pop();return data;}int top() {int size = q_.size();for (int i = 0; i < size - 1; i++) {q_.push(q_.front());q_.pop();}int data = q_.front();q_.pop();q_.push(data);return data;}bool empty() {return q_.empty();}private:std::queue<int> q_;
};2 用栈实现队列
leetcode 链接:
用栈实现队列
用栈实现队列,需要在出队的时候进行操作。在入队的时候进行操作,算法不好实现,不像队列中的元素,比如元素顺序是 E1、E2、E3、E4、E5,那么元素在移动之后还是这样的顺序,移动多次之后还是保持这样的顺序。但是对于栈来说,每移动一次就会导致顺序翻转,所以在入队的时候进行操作的算法不好实现。
使用栈实现队列,需要使用两个栈。只使用一个栈,算法也不好实现。
两个栈 A 和 B,在入队的时候只往 A 压栈,出队的时候只从 B 出栈。当 B 是空的时候,那么将 A 中所有的元素都移动到 B。
class MyQueue {
public:MyQueue() {}void push(int x) {s_in_.push(x);}int pop() {if (s_out_.empty()) {while (!s_in_.empty()) {s_out_.push(s_in_.top());s_in_.pop();}}int ret = s_out_.top();s_out_.pop();return ret;}int peek() {if (s_out_.empty()) {while (!s_in_.empty()) {s_out_.push(s_in_.top());s_in_.pop();}}return s_out_.top();}bool empty() {return s_out_.empty() && s_in_.empty();}private:std::stack<int> s_in_;std::stack<int> s_out_;
};这篇关于用队列实现栈,用栈实现队列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






