DBN---RBM简介

2024-05-25 22:48

文章标签 简介 rbm dbn

本文主要是介绍DBN---RBM简介，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

RBM

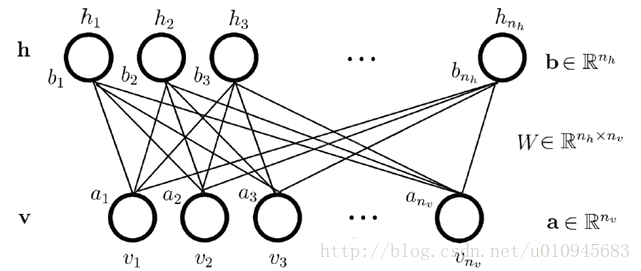
上图即是RBM(受限玻尔兹曼机)的网络结构图，与玻尔兹曼机的区别就在于没有层内连接，其中 $v$ 为可见层， $h$ 为隐藏层，可见层用于输入数据和获取结果，隐藏层则表示状态的变化，另外
$\mathbf v=(v_1,v_2,...,v_{n_{v}})$ 表示可见层神经元的状态，
$\mathbf h=(h_1,h_2,...,h_{n_{h}})$ 表示隐藏层神经元的状态，
$\mathbf a=(a_1,a_2,...,a_{n_{v}})$ 表示可见层神经元的偏置，
$\mathbf b=(b_1,b_2,...,b_{n_{h}})$ 表示隐藏层神经元的偏置，
$\mathbf W$ 则是层间连接权值矩阵

RBM是基于能量的模型(EBM)，定义了一个能量函数，能量最小时，模型达到最优，

E θ (v, h) = - \sum i = 1 n v a i v i - \sum i = 1 n h b i h i - \sum i = 1 n v \sum j = 1 n h w i, j h j v i θ = {a, b, W}

$E_\theta(\mathbf v,\mathbf h)=-\sum_{i=1}^{n_v}a_iv_i-\sum_{i=1}^{n_h}b_ih_i-\sum_{i=1}^{n_v}\sum_{j=1}^{n_h}w_{i,j}h_jv_i\\ \theta=\{\mathbf a,\mathbf b,W \}$
由此

v,h $v,h$ 间的联合概率分布可以得到，

P θ (v, h) = 1 Z θ e - E θ (v, h), 其 中 Z θ = \sum v, h e - E θ (v, h)

$P_\theta(\mathbf v,\mathbf h)={{1}\over{Z_\theta}}e^{-E_{\theta}(v,h)},\\ 其中Z_\theta=\sum_{v,h}e^{-E_{\theta}(v,h)}$

Zθ $Z_\theta$ 是相当于一个归一化因子的存在,还能得到

P θ (v) = \sum h P θ (v, h) P θ (h) = \sum v P θ (v, h)

$P_{\theta}(\mathbf v)=\sum_{h}P_{\theta}(v,h)\\ P_{\theta}(\mathbf h)=\sum_{v}P_{\theta}(v,h)$
对于后面得到更新规则，

P(vi|h)orP(hi|v) $\bbox[yellow]{P(v_i|\mathbf h) or P(h_i|\mathbf v)}$ 这个条件概率很重要.

b k (h) = a k + \sum j = 1 n h w k, j h j β (h, v v k \notin V) = \sum i = 1, i \neq k n v a i v i + \sum i = 1 n h b i h i + \sum i = 1 n v \sum j = 1, j \neq k n h w i, j h i v j

$b_k(h)=a_k+ \sum_{j=1}^{n_h}w_{k,j}h_j\\ \beta(\mathbf h,\mathbf v_{v_k \notin V})=\sum_{i=1,i \neq k}^{n_v}a_iv_i+\sum_{i=1}^{n_h}b_ih_i+\sum_{i=1}^{n_v}\sum_{j=1,j \neq k}^{n_h}w_{i,j}h_iv_j$
因此

E θ (v, h) = - β (h, v v k \notin V) - v k b k (h)

$E_\theta(\mathbf v,\mathbf h)=-\beta(\mathbf h,\mathbf v_{v_k \notin V})-v_kb_k(h)$
那么

P (v k = 1 | h) = P (v k = 1 | v i, i \neq k, h) = P ( v k = 1 , v i , i \neq k , h ) P ( v i , i \neq k , h ) = P ( v k = 1 , v i , i \neq k , h ) P ( v k = 1 , v i , i \neq k , h ) + P ( v k = 0 , v i , i \neq k , h ) = 1 Z e - E ( v k = 1 , v i , i \neq k , h ) 1 Z e - E ( v k = 1 , v i , i \neq k , h ) + 1 Z e - E ( v k = 0 , v i , i \neq k , h ) = 1 1 + e E ( v k = 1 , v i , i \neq k , h ) - E ( v k = 0 , v i , i \neq k , h ) = 1 1 + e [ β ( h , v i , i \neq k ) + 0 * b k ( h ) ] + [ - β ( h , v i , i \neq k ) - 1 * b k ( h ) ] = 1 1 + e - b k ( h ) = s i g m o i d (b k + \sum j = 1 n h w k, j h j)

$P(v_k=1|\mathbf h)\\ =P(v_k=1|v_{i,i\neq k},\mathbf h)\\ ={{P(v_k=1,v_{i,i\neq k},\mathbf h)}\over{P(v_{i,i\neq k},\mathbf h)}}\\ ={{P(v_k=1,v_{i,i\neq k},\mathbf h)}\over{P(v_k=1,v_{i,i\neq k},\mathbf h)}+P(v_k=0,v_{i,i\neq k},\mathbf h)}\\ ={{{{1}\over{Z}}e^{-E(v_k=1,v_{i,i\neq k,}\mathbf h)}}\over{{{{1}\over{Z}}e^{-E(v_k=1,v_{i,i\neq k,}\mathbf h)}}+{{{1}\over{Z}}e^{-E(v_k=0,v_{i,i\neq k,}\mathbf h)}}}}\\ ={{1}\over{1+e^{{E(v_k=1,v_{i,i\neq k,}\mathbf h)}-E(v_k=0,v_{i,i\neq k,}\mathbf h)}}}\\ ={{1}\over{1+e^{[\beta(\mathbf h,\mathbf v_{i,i\neq k})+0*b_k(h)]+[-\beta(\mathbf h,\mathbf v_{i,i\neq k})-1*b_k(h)]}}}\\ ={{1}\over{1+e^{-b_k(h)}}}\\ =sigmoid(b_k+ \sum_{j=1}^{n_h}w_{k,j}h_j)$
由此得到