本文主要是介绍【机器学习300问】97、机器学习中哪些是凸优化问题,哪些是非凸优化问题?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在机器学习的领域中,多数模型的参数估计问题实质上可以转化为优化问题。鉴于机器学习模型的多样性,不同的模型会对应着不同的损失函数,进而形成各具特色的优化问题。了解优化问题的形式和特点,对于提升我们求解模型参数的效率和准确性至关重要,从而确保机器学习模型能够达成预期的学习目标。
一、什么是凸优化问题?
(1)定义
在机器学习中,凸优化问题是指那些目标函数为凸函数,并且约束条件(如果有)定义的区域也为凸集的问题。
这类问题有很好的性质,比如全局最优解是唯一的,并且任何局部最优解都是全局最优解,这使得它们可以通过一些高效的优化算法如梯度下降、牛顿法或拟牛顿法等来求解。
(2)凸函数
凸函数指的是在其定义域内任意两点连线上的值总是处于这两点在函数上对应值的连线之上(或等于)的函数。

用数学公式凸函数:
对于一个定义在实数集合上的函数 ,如果对于所有
和任意
,下面的不等式始终成立:
那么,函数就是一个凸函数。 这个定义意味着,如果你取定义域内的任意两点
和
,以及这两点之间的任意加权平均
,函数在这个加权平均上的值不大于这两点对应函数值的加权平均。
(3)凸集
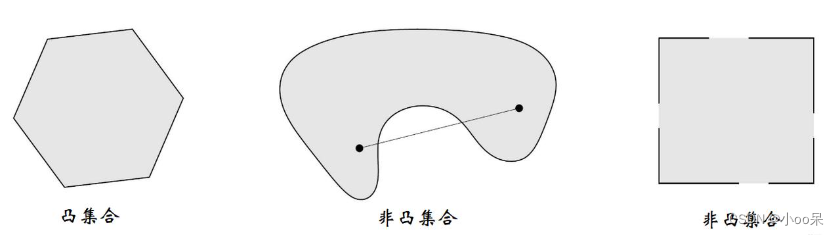
凸集是欧几里得空间中的一个子集,如果集合内任意两点间的线段完全包含在这个集合内,则该集合是凸集。
想象你有一块没有洞,边界也不弯曲到内部的物体,如果你任意选择该物体内的两点并连接它们,这根连线完全位于物体内部,那么这个物体就是一个凸集合的形状实例。
用数学语言来表达,一个集合是凸集,如果对于集合中的任意两点
,下面的条件对所有
满足
都成立:
二、哪些是机器学习中的凸优化问题?
- 线性回归:当使用均方误差作为损失函数时,线性回归成为一个凸优化问题。
- 逻辑回归:在 logistic 函数下的最大似然估计同样形成一个凸优化问题。
- 支持向量机(SVM,线性核):硬间隔或软间隔的支持向量机,当使用线性核函数时,目标是最小化 hinge 损失或拉格朗日函数,这是一个凸优化问题。
- 最小二乘问题:在没有额外约束的情况下,是最基本的凸优化问题之一。
三、哪些是机器学习中的非凸优化问题?
非凸优化问题指的是目标函数不是凸函数,或者约束条件定义的区域不是凸集的情况。在这些情况下,寻找全局最优解更加困难,因为可能存在多个局部最优解或鞍点。
- 非线性支持向量机:使用非线性核函数(如RBF核)时,虽然原始问题转换到特征空间后可能是凸的,但在原始参数空间中的问题是非凸的。
- 神经网络:多层神经网络的损失函数通常是非凸的,尤其是当使用激活函数如ReLU时,这导致了优化问题的复杂性。
- 主成分分析(PCA):尽管PCA的目标函数(通常是数据协方差矩阵的迹减去各个特征值之和)是凸的,但其约束(保持变换后的数据方差最大化同时保持正交投影矩阵)形成了一个非凸集合,因此整体问题被视为非凸优化问题。
- 非负矩阵分解:当限制因子矩阵中的元素非负时,问题变为非凸。
这篇关于【机器学习300问】97、机器学习中哪些是凸优化问题,哪些是非凸优化问题?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






