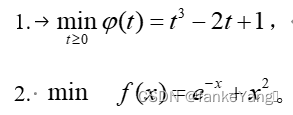非精确线搜索步长规则 在数值优化中，线搜索是一种寻找合适步长的策略，以确保在目标函数上获得足够的下降。如最速下降法，拟牛顿法这些常用的优化算法等，其中的线搜索步骤通常使用Armijo规则、Goldstein规则或Wolfe规则等。 设无约束优化问题： min ⁡ f ( x ) , x ∈ R n \min f(x),{\kern 1pt} \,x \in {R^n} minf(x),x∈R

0.618代码如下： import math # 定义函数h(t) = t^3 - 2t + 1 def h(t):     return t**3 - 2*t + 1 # 0.618算法 def golden_section_search(a, b, epsilon):      ratio = 0.618      while (b - a) > epsilon

0.618代码如下： import math # 定义函数h(t) = t^3 - 2t + 1 def h(t):     return t**3 - 2*t + 1 # 0.618算法 def golden_section_search(a, b, epsilon):      ratio = 0.618      while (b - a) > epsilon