🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨ 🌲 作者简介：硕风和炜，CSDN-Java领域优质创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻

AcWing 785. 快速排序 文章目录 题目描述C++Go模板 题目描述 给定你一个长度为 n 的整数数列。 请你使用快速排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。 输入格式 输入共两行，第一行包含整数 n。 第二行包含 n 个整数（所有整数均在 1∼10^9 范围内），表示整个数列。 输出格式 输出共一行，包含 n 个整数，表示排好序

http://codeforces.com/contest/785/problem/D 题意：给一堆括号，求有多少种规范的括号 假如说这样： ()( ( ) ( ()( ( ( (())))())))()))) 考虑每个括号的贡献，假如现在考虑第一个红色括号的贡献： 他的前面有 2 2 2 个 (((，后面有 4 4 4 个))) 考虑只配对成1对：他的前面选 0 0 0

C. Palindrome Basis 题意 定义一个正整数 a a a 是回文的（没有前导 0 0 0）当且仅当： a a a 的十进制表示形式回文 给定一个正整数 n n n ，求出将 n n n 拆分成若干个回文数之和的方案数 思路 这是一个经典模型，与爬楼梯问题不同的是：这道题一个物品的选择先后顺序无关 在 n ≤ 4 ⋅ 1 0 4 n \leq 4 \cdot

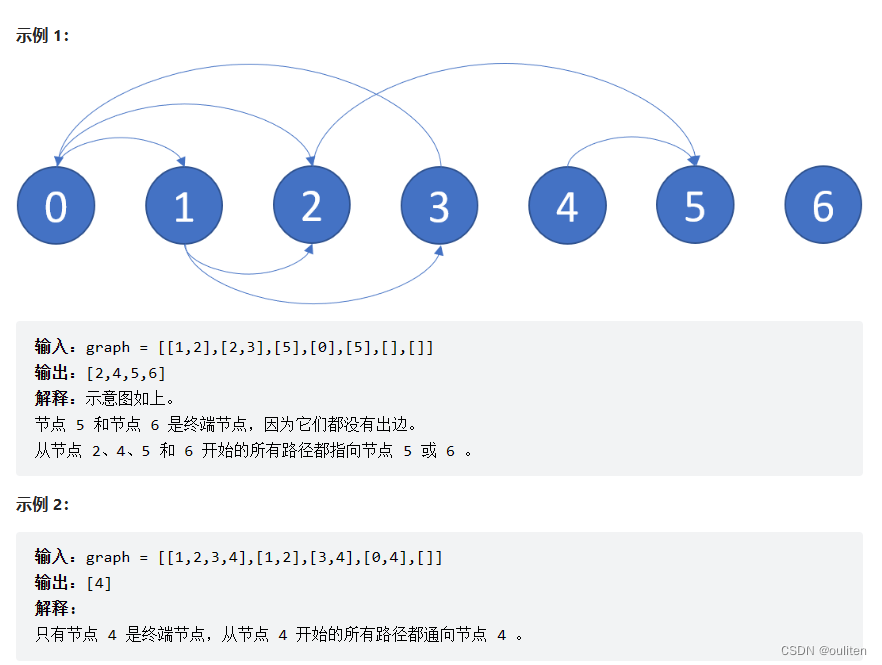
存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性： 不存在自环（graph[u] 不包含 u）。不存在平行边（grap