修改read_conn文件 static long read_conn(struct mg_connection *c) {long n = -1;// if (c->recv.len >= MG_MAX_RECV_BUF_SIZE) {// mg_error(c, "max_recv_buf_size reached");// } else if (c->recv.size - c->re

阿里云服务器3M固定带宽是什么意思？速度快吗？3M固定带宽是指云服务器的公网带宽，用于在外网提供服务的，3M带宽的下载速度是384KB/秒，上传速度是1280KB/秒，对于个人博客或流量不多的企业官网速度还是挺快的，阿里云服务器网aliyunfuwuqi.com如果是Web网站应用，网站如果接入CDN会更快，完全够用。 3M固定带宽：固定带宽是指IDC服务器提供固定速度的网络服务，公网带宽从1M

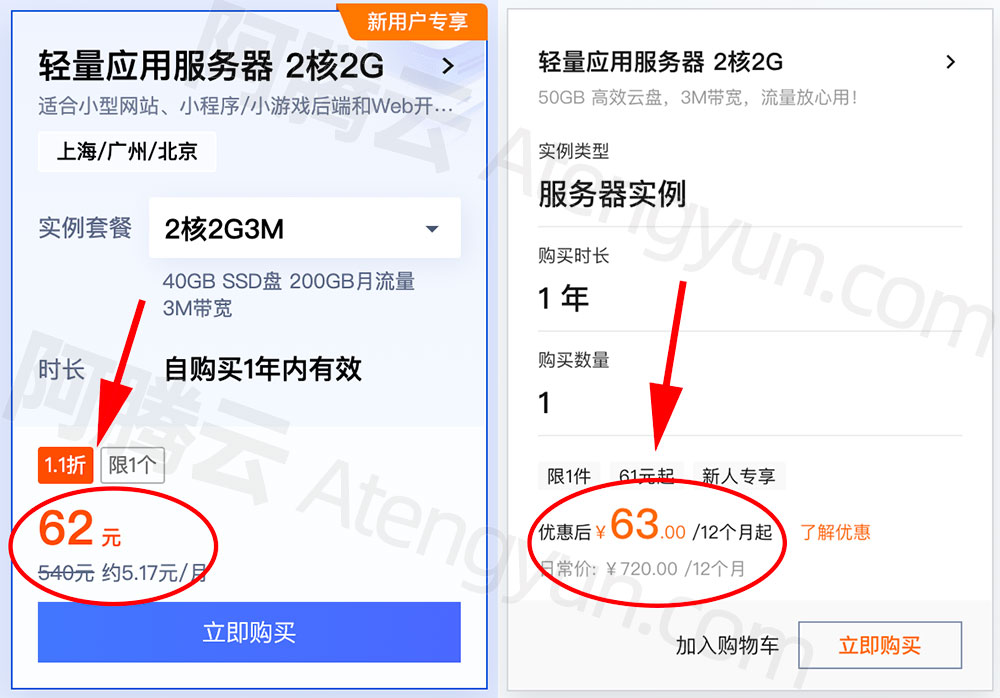
轻量应用服务器2核2G3M带宽配置阿里云和腾讯云都降价了，阿里云63元一年，腾讯云62元一年，到底选哪家比较好？这个价都需要新用户资格，第一次购买云服务器的用户，所以，如果你的账号是新用户，随便买一家都是赚的，但要是具体对比的话，阿里云不限制月流量，腾讯云限制200GB月流量，这一点倒是挺大的区别。阿腾云atengyun.com来详细对比下阿里云和腾讯云2核2G3M带宽轻量应用服务器： 腾讯云和

阿里云服务器3M带宽下载速度是384KB/秒，上传速度是1280KB/s（折合1.25M/秒），3M固定带宽够用吗？对于一般流量不是太大的个人博客、企业官网、论坛社区、小型电商网站或搭建个人学习环境或测试环境是完全够用的，以Web网站应用为例，图片视频文件可以托管到对象存储OSS上，网站接入CDN，3M公网带宽是完全够用的，像阿里云服务器网aliyunfuwuqi.com使用的是1M公网带宽，感觉

阿里云服务器3M带宽下载速度是384KB/秒，上传速度是1280KB/s（折合1.25M/秒），3M固定带宽够用吗？对于一般流量不是太大的个人博客、企业官网、论坛社区、小型电商网站或搭建个人学习环境或测试环境是完全够用的，以Web网站应用为例，图片视频文件可以托管到对象存储OSS上，网站接入CDN，3M公网带宽是完全够用的，像阿里云服务器网aliyunfuwuqi.com使用的是1M公网带宽，感觉

本周企业最新财报汇总。 科技 中芯国际2020年第四季度销售额为9.811亿美元 国际主要半导体代工制造商中芯国际集成电路制造有限公司（上交所科创板证券代码：688981，香港联交所：00981，美国场外市场：SMICY）公布截至2020年12月31日止三个月的综合经营业绩。2020年第四季的销售额为9.811亿美元，相比2020年第三季为10.825亿美元，2019年第四季为8.394亿美元。

设 m , n m,n m,n 和 p p p 为正整数。证明：多项式 g ( x ) = x 2 + x + 1 g(x)=x^2+x+1 g(x)=x2+x+1 整除多项式 f ( x ) = x 3 m + x 3 n + 1 + x 3 p + 2 f(x)=x^{3m}+x^{3n+1}+x^{3p+2} f(x)=x3m+x3n+1+x3p+2. 将 f ( x ) f(x

欢迎关注我的CSDN：https://spike.blog.csdn.net/ 本文地址：https://spike.blog.csdn.net/article/details/132978866 Paper: DPM-Solver++: Fast Solver for Guided Sampling of Diffusion Probabilistic Models 扩散概率模型