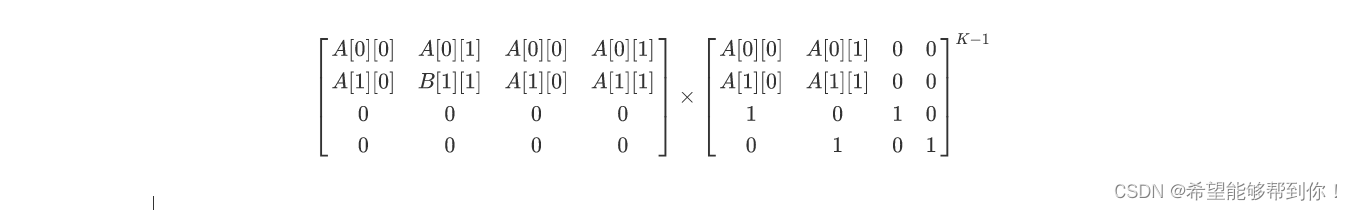题意 ：给出n k m 和一个n*n的矩阵A 求A + A2 +A3 + … + Ak 参考http://blog.csdn.net/wangjian8006/article/details/7868864 构造矩阵很重要啊！！！ 弱菜不会啊 #include <cstdio>#include <cstring>const int mod = 10000;const int maxn

Description Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak. Input The input contains exactly one test case. The first line of input contains three

这题是矩阵相乘，由于k很大，所以要借用整数快速幂（如果不会快速幂可以参看我之前的博文）的方法计算矩阵的相乘，所以方法与之前的差不多，如果这个会了，题目就不难了。这道题有更高级的方法，但是我用的是普通的方法，也能AC，适合初学者。         这道题我主要是写了矩阵相乘、相加和n次方，这不难理解。这道题用了一个小技巧，就是用struct“包装”了二维数组，这样返回矩阵和赋值将会

poj 1575  Tr A 题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1575 题目大意：A为一个方阵，则Tr A表示A的迹（就是主对角线上各项的和），现要求Tr(A^k)%9973。 数据的第一行是一个T，表示有T组数据。 每组数据的第一行有n(2 <= n <= 10)和k(2 <= k < 10^9)两个数据。接下来有n行，每行有n

Matrix Power Series http://poj.org/problem?id=3233 Time Limit:  3000MS Memory Limit: 131072K Description Given a n × n matrix A and a positive integer k, find the

题目链接：http://poj.org/problem?id=3233 题意：已知一个n*n的矩阵A，和一个正整数k，求。 分治思路：首先我们知道  可以用矩阵快速幂求出来。其次可以对  进行分治，每次将规模减半，如下： ： 。   ： 。   :   。 从上面几个式子可以发现，当k为奇数或者偶数的区别。 对于一个  是偶数则：。 如果  为奇数的话需要加上也就是：。 #i

世界树 金牌导航 虚树-1 luogu 3233 题目大意 对于一棵树，给出若干询问，每个询问告诉你若干个特殊点，对于所有点，都会选择离自己最近（距离相等就选编号最小的）的特殊点，问对于所有特殊点，有多少个点选择该点 输入样例 10 2 1 3 2 4 3 5 4 6 1 7 3 8 3 9 4 10 1 5 2 6 1 5 2 7 3 6 9 1

3233 古道时间限制: 1 s空间限制: 8000 KB题目等级:**白银 Silver**[传送门](http://codevs.cn/problem/3233/)题目描述 Description【第2天】小陈坐车3个小时，终于到达了风光旖旎的云水谣古道。从它的入口开始，有N种风景，例如千年的大榕树、河上的瀑布，河边的沙滩。。。。。。每种每隔ai米有一个，所有风景交汇在一点的地方是"

一、题目大意 给出一个矩阵A， 输出矩阵B的每一项对M取余数的值。 二、解题思路 以二维矩阵为例，首先计算K=2的情况，我们设结果矩阵为B 有如下表达式 那么不难看出，需要的矩阵其实就是以下的两个矩阵相乘后的左上角的N*N个 然后我们再来考虑K=3的情况，我们设结果矩阵为C 我们来考虑如何把C表示成矩阵B和A相乘的状态。 不难看出C矩阵就是以下两个矩阵相乘后的N*