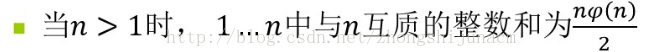GCD(一) 题目：  The greatest common divisor GCD(a,b) of two positive integers a and b,sometim

hdu 2588 GCD http://acm.hdu.edu.cn/showproblem.php?pid=2588 大意： Given integers N and M, how many integer X satisfies 1<=X<=N and (X,N)>=M. 分析：已知(a,b)=k  --> (a/k, b/k)=1 所以，问题即是求解有多少个x

我沙茶 我沙茶 我沙茶 傻到去写链剖！ 本来求个LCA又好写又快..... #include <cstdio>#include <iostream>#include <algorithm>using namespace std;#define MAXN 100010int team[MAXN],head,tail;int fa[MAXN],son[MAXN],size[M

点击打开链接 对于一个数n 在比它小的数中 除了他的因子 其他数和n的gcd均为1 所有符合题意的数x肯定是n的某个因子的倍数 所以只用看n的所有因子 假设有一个n的因子p大于m 就看（n/p）的欧拉函数值是多少 累加 至于为什么要求（n/p）的欧拉函数 这是为了解决”冲突“ 对于n的因子p和一个与（n/p）不互素的k  k*p就会变成n的其他因子或其他因子的倍数 这里需要仔细想想 #in

2588: Spoj 10628. Count on a tree Time Limit: 12 Sec Memory Limit: 128 MB Description 给定一棵N个节点的树，每个点有一个权值，对于M个询问(u,v,k)，你需要回答u xor lastans和v这两个节点间第K小的点权。其中lastans是上一个询问的答案，初始为0，即第一个询问的u是明文。 Input

本文研究全球市场、主要地区和主要国家低聚糖的销量、销售收入等，同时也重点分析全球范围内主要厂商（品牌）竞争态势，低聚糖销量、价格、收入和市场份额等。   针对过去五年（2017-2021）年的历史情况，分析历史几年全球低聚糖总体规模，主要地区规模，主要企业规模和份额，主要产品分类规模，下游主要应用规模等。规模分析包括销量、价格、收入和市场份额等。针对未来几年低聚糖的发展前景预测，本文预测到202