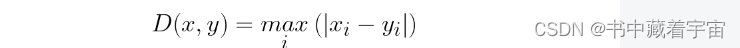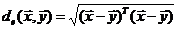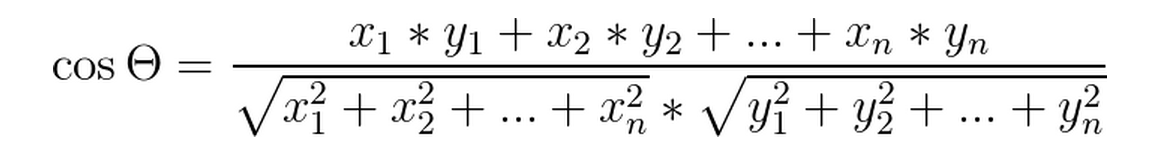在深度学习以及图像搜索中，经常要对特征值进行比对，得到特征的相似度，常见的特征值比对方法有汉明距离、余弦距离、欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等，下面对各种比对方法分别进行介绍。 目录 1汉明距离 2余弦相似度 3欧式距离 4曼哈顿距离 5切比雪夫距离 6闵可夫斯基距离 7马氏距离 1汉明距离 汉明距离/Hamming Distance也能用来计算两

DeepSORT（目标跟踪算法）中的马氏距离详解（很详细） flyfish 马氏距离的公式是由印度统计学家【普拉萨纳·钱德拉·马哈拉诺比斯（Prasanta Chandra Mahalanobis）】）（好长的名字，抄的）在1936年提出的。马氏距离是一种多维尺度上的距离度量，它考虑了各个维度之间的相关性，并且通过协方差矩阵对数据进行缩放，使得在计算不同数据点之间的距离时，可以考虑到各个维度的

近红外光谱（NIR）技术在许多领域中都有广泛应用，包括食品、医药和化工等。然而，由于其高维特性，NIR数据分析常常面临诸多挑战。为了更有效地处理这些数据，降维技术和异常值检测方法变得尤为重要。本文将介绍如何利用主成分分析（PCA）和马氏距离结合，剔除NIR数据中的异常值。 （1）数据预处理 首先，导入并标准化NIR数据。标准化是将数据转换为均值为0，标准差为1的形式，有助于提高PCA的效果。标

文章目录 一、简介二、算法步骤三、代码实现四、实现效果参考资料 一、简介 在诸多的聚类方法中，K-Means聚类方法是属于“基于原型的聚类”(也称为原型聚类)的方法，此类方法均是假设聚类结构能通过一组原型刻画，在现实聚类中极为常用。通常情况下，该类算法会先对原型进行初始化，然后再对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式，也将会产生不同的算法。 K-Mea

目录 一、 余弦相似度（Cosine Similarity） 1、简介 2、代码实现 二、汉明距离（Hamming Distance） 1、简介 2、代码实现 三、马氏距离（Mahalanobis Distance） 1、简介 2、代码实现 四、编辑距离（Levenshtein Distance） 1、简介 2、代码实现 一、 余弦相似度（Cosine Similar

数据间的各种距离 欧几里得距离代码 哈曼顿距离距离代码 切比雪夫距离代码 余弦距离距离代码 相关系数距离代码 马氏距离代码 数据表来源于：链接: link 欧几里得距离 代码 from scipy.spatial import distancedist1 = distance.cdist(me_data,me_data,'euclidean')print

Mahalanobis distance In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936.It is based on correlations （相关性）between variables by which different patterns

基础知识： 假设空间中两点x，y，定义： 欧几里得距离，

使用 检查水平向斜视时，使用水平向马氏杆检查;重直向斜视时，使用重直问马氏杆;检查旋转斜视时，使用双马氏杆. 检查水平向斜视 双眼屈光不正全矫 双眼同时打开，右眼前加水平向马氏杆，左眼前不加 双眼同时观察点光源，左眼看点，右眼看一条竖线 点线重合则无水平向斜视线在左边，点在右边则有外斜，应加 BI 棱镜至线与点重合线在右边，点在左边则有内斜，应加 B0 棱镜至线与点重合 检查垂直向斜

目录 1.欧式距离EuclideanDistance 2. 曼哈顿距离(ManhattanDistance) 3. 夹角余弦 4.汉明距离(Hamming Distance)     1.欧式距离EuclideanDistance 欧式距离：也称欧几里得距离，在一个N维度的空间里，求两个点的距离，这个距离肯定是一个大于等于零的数字，那么这个距离需要用两个点在各自维度上的坐标