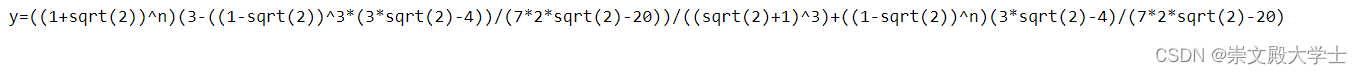递推关系为a(n) ​=pa(n−1) ​ +qa(n−2) ​，本项=前一项*2+前前项，具体如 1，1，3，7，17，41，99，239，…… 一般的递推关系可以用以下方法 得两个解： 用第3项、第4项组两个方程： 解方程的结果 解方程的链接：https://mathdf.com/equ/cn/ Excel验证，有误差，是复杂的计算导致精度丢失： python验证 impo

习题来源：《基础数论》[(美)杜德利 著] 译者:周仲良 附录一：习题7 题： 假定，且对n=1,2,…,有,用归纳法证明： 这里先解出通项公式的推导过程，然后再证明通项公式的n的范围 解1： 由变形：知：为首项为2，公比为2的等比数列： 列出各项： 。 解2： 。 归纳法证明通项的正确性，晚上写。。

一、引例  我们知道，对于正项级数可以利用所谓的通项等价关系进行审敛，即 废话不多说，看例题 ：  二、经错标零 例题你觉得简单？下面这坑你必踩~ 经典的错误，标准的零分~  关注A选项~ 你的做法： 应用性质：在级数中加上或减去有限项后级数的敛散性不变 设从某一项 N 之后， 运用等价无穷小 如果按照交错级数审敛法(莱布