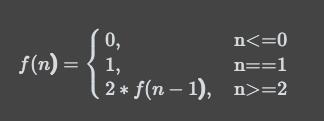Colmerauer Accepts: 32 Submissions: 121 Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) 问题描述 Peter有一个n \times mn×m的矩阵MM. 定义S(a,b)S(a,b)为

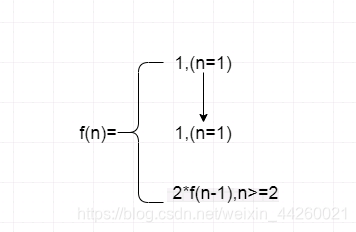
分析： f(1) = 1 f(2) = f(2-1) + f(2-2) //f(2-2) 表示2阶一次跳2阶的次数。 f(3) = f(3-1) + f(3-2) + f(3-3) … f(n) = f(n-1) + f(n-2) + f(n-3) + … + f(n-(n-1)) + f(n-n) 说明： 1）这里的f(n) 代表的是n个台阶有一次1,2,…n阶的 跳法数。 2）n = 1时，只

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。 其实就是斐波那契数列问题。 假设f(n)是n个台阶跳的次数。 f(1) = 1 f(2) 会有两个跳得方式，一次1阶或者2阶，这回归到了问题f(1),f(2) = f(2-1) + f(2-2) f(3) 会有三种跳得方式，1阶、2阶、3阶，那么就是第一次跳出1阶后面