角频率专题
笔记-模拟角频率和数字角频率的关系理解
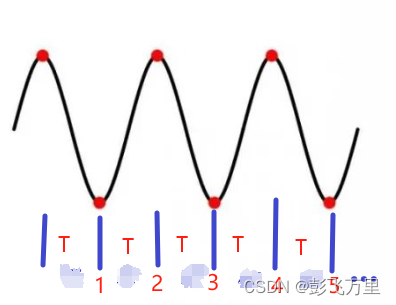
先建议阅读前人此文(点击这里),有助于理解。 模拟频率:f 模拟角频率:Ω 数字角频率:ω 其中:在模拟信号中Ω = 2πf 正弦波表示:sin(2πft) = sin(Ωt) 数字信号就是离散的,由一个个点构成,如下红点所示,T是采样时间,其倒数为采样频率,即fs = 1/T 此时模拟信号的时间t也离散了,变成一个个点,分别对应 1T,2T,3T,… 即t = nT (n =0,1,2,
陈后金版本的模拟角频率与数据角频率区别
第一眼看这个时域抽样定理用到模拟角频率和数字角频率的画图,可能会不理解,下面提供两种方法,对比连续函数(模拟)和离散函数的角频率区别就可理解陈老师的讲解: 我们由时域抽样定理可知: 还有一种简单的理解方法如下:
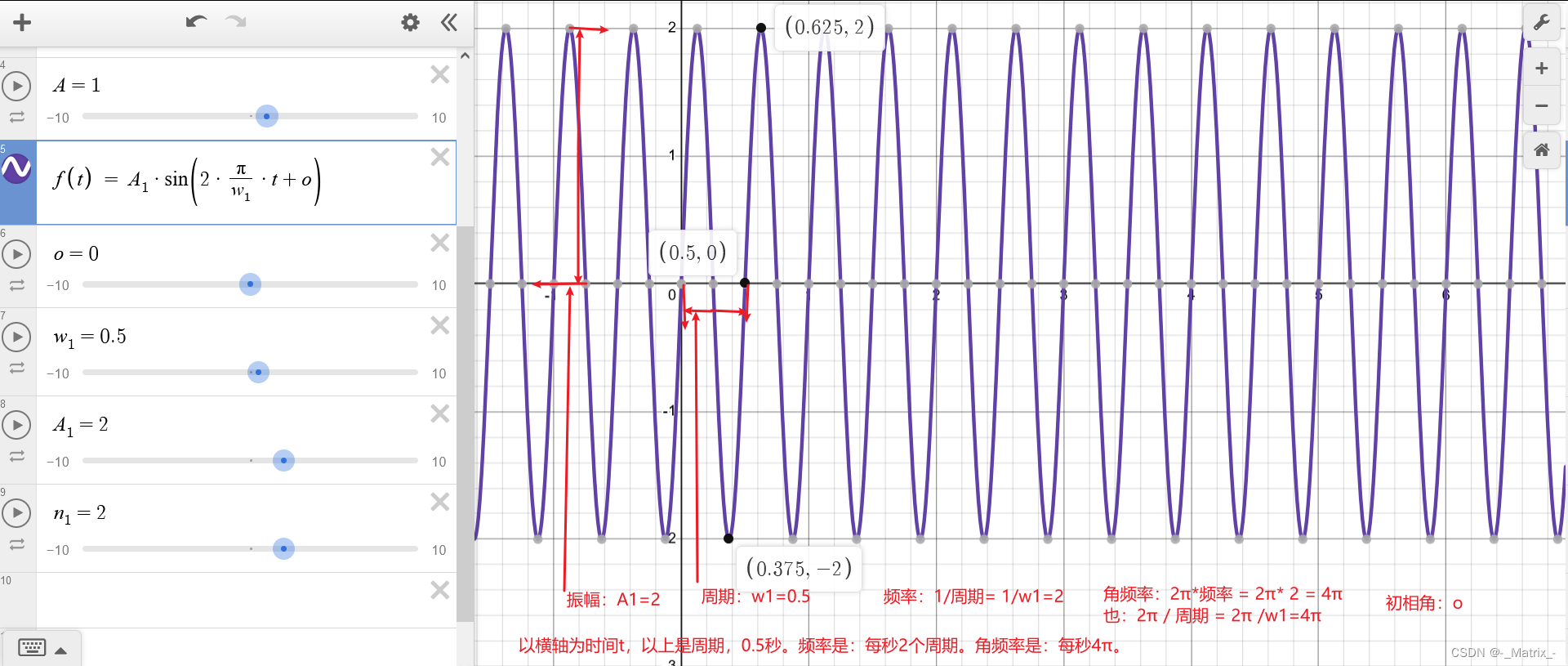
周期 角频率 频率 振幅 初相角
文章目录 周期 角频率 频率 振幅 初相角相位差 周期 角频率 频率 振幅 初相角 当我们谈论傅里叶级数或波形分析时,以下术语经常出现: 周期 T T T: 函数在其图形上重复的时间或空间的长度。周期的倒数是频率。 频率 f f f: 周期的倒数,即一秒内波形重复的次数。单位通常为赫兹(Hz)。 f = 1 T f = \frac{1}{T} f=T1