///定义: /*     排列组合解决球盒的八大问题，其中用到排列组合公式和第二类斯特林公式 */ ///代码： /***name:第二类斯特林数（第二类Stirling数）**function:解决求不同盒同等问题**公式： S(r, c) = S(r-1,c-1) + c * S(r-1, c)*/#include <iostream>#inclu

说明：本博文来自CSDN-问答板块，题主提问。 需要：球和盒子 设有n个球，m个盒子。将球是否相同，盒子是否相同，是否可以有空盒（有空盒指的是可以有空盒）分为八种情况。写出将球放入盒子的所有情况求法，并选择其中2个，写出相应的程序代码。（用两种语言写），可以使用python、java、C、C++编写。     一、解决方案 这是一个组合数学中常见的问题。8种情况具体为： 球相

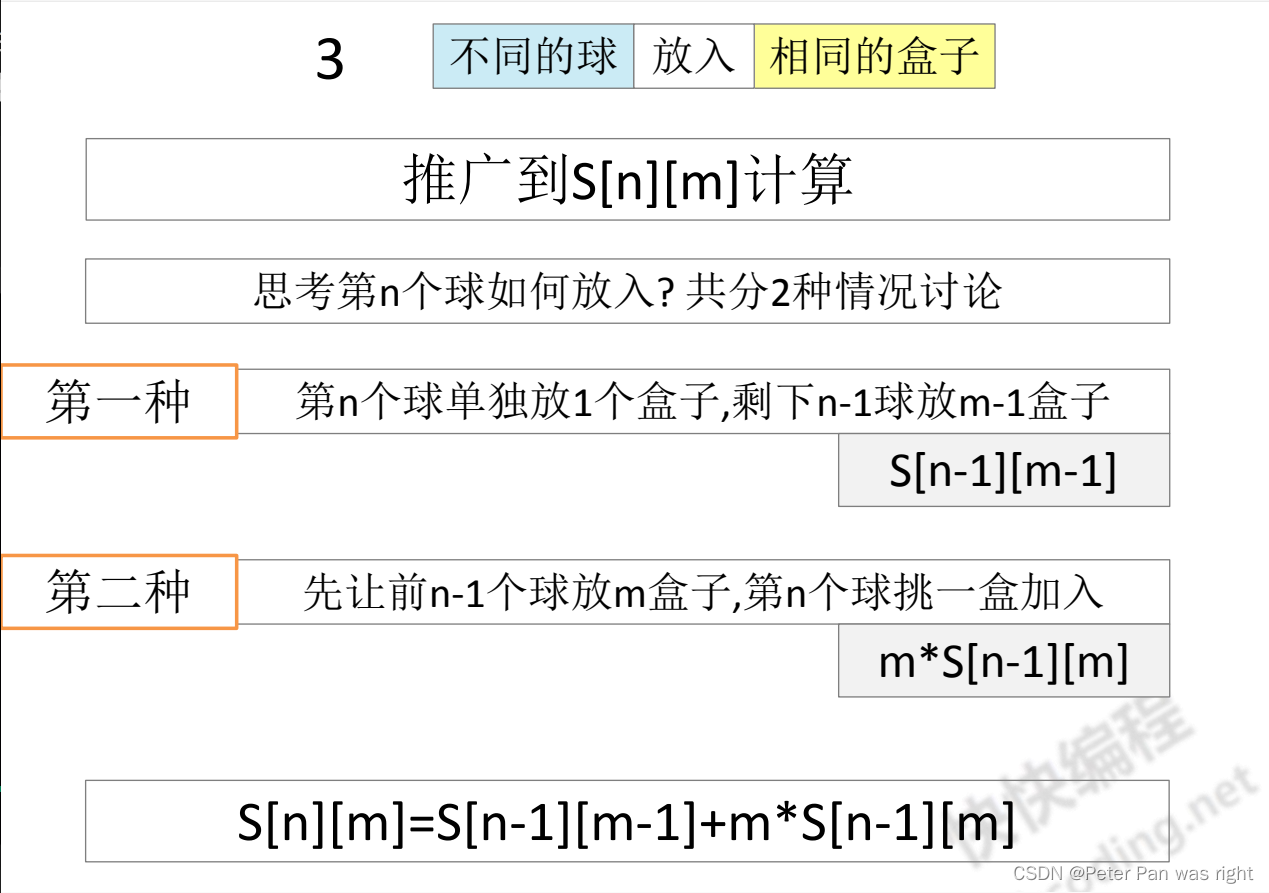
球盒问题有8类，分别如下图 相同的球放入相同的盒子 根据上一篇Peter算法小课堂—正整数拆分-CSDN博客 简单来说，就这样👇  将相同的球放入相同的盒子，其实相当于将正整数i分为j个正整数的个数 cin>>n>>m;if(n<m){cout<<0<<endl;return 0;}for(ll i=2;i<=n;i++) f[i][1]=1;for(ll j=2;j<