目录 1.第 N 个泰波那契数1.题目链接2.算法原理详解3.代码实现 2.三步问题1.题目链接2.算法原理详解3.代码实现 3.使用最小花费爬楼梯1.题目链接2.算法原理详解3.代码实现 4.解码方法1.题目链接2.算法原理详解3.代码实现 1.第 N 个泰波那契数 1.题目链接 第 N 个泰波那契数 2.算法原理详解 题目解析： 思路： 确定状态表示 -

目录 【动态规划理论基础】 【509. 斐波那契数】简单题 方法一  用额外的数组存储每个状态 方法二  用2个遍历存储前两个状态（减小空间复杂度） 【70. 爬楼梯】简单题 【746. 使用最小花费爬楼】简单题 【动态规划理论基础】 1、定义：英文为Dynamic Programming，简称DP 2、步骤： 确定变量 f(i) 的含义确定递推公式：如 f(i) 和 f

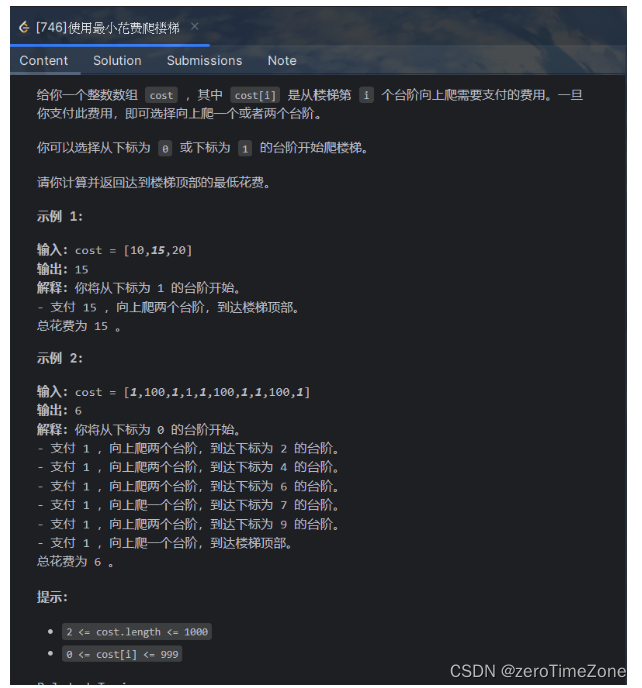
//给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。 //// 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 //// 请你计算并返回达到楼梯顶部的最低花费。 //// //// 示例 1： //// //输入：cost = [10,15,20]//输出：15