1、介绍 先上张图来说明用回溯法解八皇后问题的每一步：          2、程序 看着严蔚敏的书写的，写好后运行一次性成功了，程序如下： // N皇后问题 #include <iostream> using namespace std; #define N 8 bool matrix[N + 1][N + 1] = {0}; bool IsLegal(

回溯法解旅行商问题(TSP) 旅行商问题,常被成为旅行推销员问题,是指一名推销员要拜访多个地点,如何找到再拜访每个地点一次后再回到起点的最短路径. 进一步的抽象,可以转化为图论的问题,将每个城市看成图 G(V,E) 中的一个顶点,则旅行商问题可以转化为从一个顶点s出发,找到一条最短的路径从s出发,经过所有的顶点,最后回到s.最简单的解法就是枚举,枚举所有的路径,计算其每条路径的长度,

目录 介绍一下TSP问题 介绍一下哈密顿回路 介绍一下解空间树 回溯法解TSP问题时的解空间树为什么是子集树 斯德哥尔摩综合征 病因 临床表现 历史记录 介绍一下TSP问题 TSP问题，即旅行商问题（Traveling Salesman Problem），是一个经典的组合优化问题12。它可以描述为：假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每

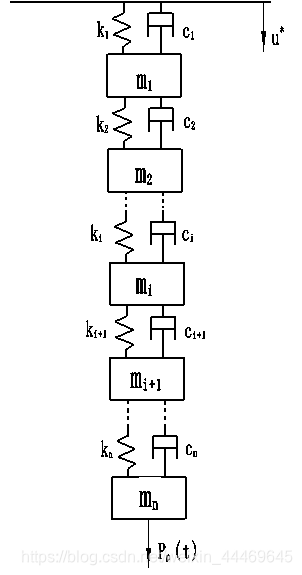
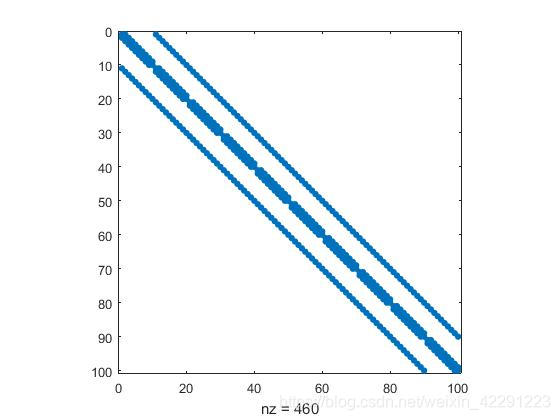
@[TOmatlab编的龙格库塔法解微分方程，求改错 数学模型： 主程序数据： R1=0.019; R2=0.022; R3=0.044; R4=0.062;% 一级杆直径，二级杆直径，泵径,油管径 L1=1100; L2=500; %L1碳纤维杆的长度，L2钢杆长度 L=5; %单元节长 h1=1600;h2=1047; %泵挂深度 ，动液面 hc=h1-h2; %泵沉没度 S1=1900;

概念：   回溯法采用深搜+剪枝来搜索生成树： 步骤： 1. 假设规定左叉标1（代表选择该物品装入背包），右叉标0（代表不选择该物品装入背包）。给定示例输入： 背包容量c=10 物品个数n=5 物品重量w={2，2，6，5，4} 物品价格p={6，3，5，4，6} 注意：     左子树的解的上界与父节点相同，不用计算。右子树的解的界值：较好的就算方法是将剩余物品依其单位重量价

暑假过了一半多了，前几天看到八皇后问题，就写了出来，使用回溯法。 八皇后问题：在8*8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 思路：简单的说就是 从当前列中依次选取位置，与前面列中选取的位置进行比较，判断是否冲突，若冲突，回溯到上一列寻找，否则进入下一列寻找位置 　　　1、从column=0列中选取一个位置，column

this.p={ m:2, b:2, loftPermalink:'', id:'fks_084069082082088064084087085095085086087068093080080065', blogTitle:'Adams预估计-校正法解微分方程', blogAbstract:'Adams预估计-校正法解微分方程。\r\n\r\nfunction T=Adams_PreEs(f,a

算法思想 如何利用电子计算机来快速、有效地求解线性方程组是数值线性代数研究的核心问题，而且也是目前人在继续研究的重大课题之一。 Cholesky分解法又叫做平方根法，是求解对称正定线性方程组最常用的方法之一。A是一个对称正定的矩阵，则存在一个对角元均为正数的下三角阵L,使得A=LL’，称为Cholesky分解，而后我们可以由下面三步求解： (1)计算A的Cholesky分解：A=LL’； (2)