要求的时间需要晚于当前时间且和当前时间最近。时间串里一共四个数字字符，做全排列即可，使用到回溯算法。把时间串里的“：”剔除后，做回溯爆搜，每取4个字符就判断一次：1.作为时间串是否合法；2.如果合法，反应到最终结果中去； 特殊处理1：当以输入时间串得不到更大的时间时，说明比当前时间更晚的是第二天的时间，又要求这个时间离当前时间最近，所以直接取能得到的最小时间即可。 特殊处理2：当输入“00：0

C++11 STL内置了求全排列的模板函数next_permutation和prev_permutation，属于<algorithm>头文件和std命名空间，使用非常方便。例如： vector<int> A{1,2,3,4,5};while (next_permutation(A.begin(),A.end()){cout<<A[0]<<A[1]<<A[2]<<A[3]<<A[4]<<en

本文取自July的《编程之法》一书。 求n个字符的n！个全排列。 解法一：        从字符串中选出一个字符作为排列的第一个字符，然后对剩余的字符进行全排列。如此递归处理，从而得到所有字符的全排列。如字符串为“abc”，按一下步骤进行。 将a固定在第一位，求后面bc的排列，得到：“abc”和“acb”。将b固定在第一位，求后面ac的排列，得到：“bac”和“bca”。将c固定在第一

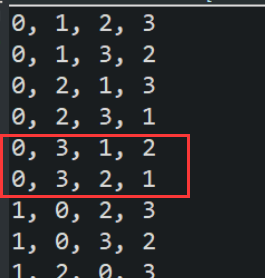
递归法 假设我们有0，1，2，3四个数需要全排列，递归法是一种比较类似于深度搜索的方法，直到递归最深处，才得出结果。 其大概思路是，设置一个游标start，游标所到之处，其左侧已经考虑过，利用递归思想求剩下的全排列。 仔细分析，依次考虑每一位数。由于对于每一位数，它可能的数包括除了之前考虑过的所有数，因此将start右侧（包括start）的所有数都和start这一位交换一次，每交换后，马上进

版本1：非常像八皇后问题，请参见博客：https://blog.csdn.net/u011426016/article/details/88818754 八皇后要求不在同一行、同一列、以及同一条对角线上，这里只要求不在同一行，同一列即可。同一行自然不可能，因为每个皇后单独放置一行，同一列很好检查，使用visit数组标记即可，这种方法的优点是如果初始序列有序的话，可以保证全排列按字典序递增排列。