来讲专题
对开发来讲,业务重要还是技术重要?
很多开发者为天天写业务代码无暇提升技术而焦虑、苦恼,比如: 又如: 又如: 再如: 那么,作为开发者,到底该怎么面对“写业务代码”这件事呢? 今天我们就从以下几个方面聊聊这个话题: 什么是业务业务和技术的关系业务和因解决业务而衍生的业务对业务的态度因你在团队中的角色而不同如何从写业务代码中跳出来,做你所谓的有技术含量的工作 我们先来看看,什么是业务。 1. 什么是业
将Excel导入MSSQL2000时出现对于所指定的缓冲区来讲太大错误的解决方法?
将一个EXCEL表格导入数据库时总是报错,开始以为是数据过长,但不管如何修改数据类型也不行.于是在网上查到解决方法: 在源的行号为 9 处出错。到目前为止,在该任务中遇到错误数: 1 作为源列 86(“内容简介”)的数据对于所指定的缓冲区来讲太大 解决办法: 修改服务器的注册表: HKEY_LOCAL_MACHINE/SOFTWARE/Microsoft/Jet/4.0/Engine
对于互联网公司来讲,定位自身角色是其穿越周期的关键所在
如果你仅仅只是还在用以往的眼光来看待腾讯,那么,或许是无法完全理解腾讯能够穿越一个又一个周期的内在逻辑的。 按照以往的思维,所谓的腾讯,仅仅只是一个以社交、游戏为主导的存在。 无论是微信的风靡,还是《王者荣耀》的全民化,无一不是这样一种现象的直接体现。 然而,这,却并不是真正意义上的腾讯。 特别是在各色互联网玩家们都在转型的大背景下,仅仅只是以社交、游戏等固有的传统业务来定义腾讯,愈发显得
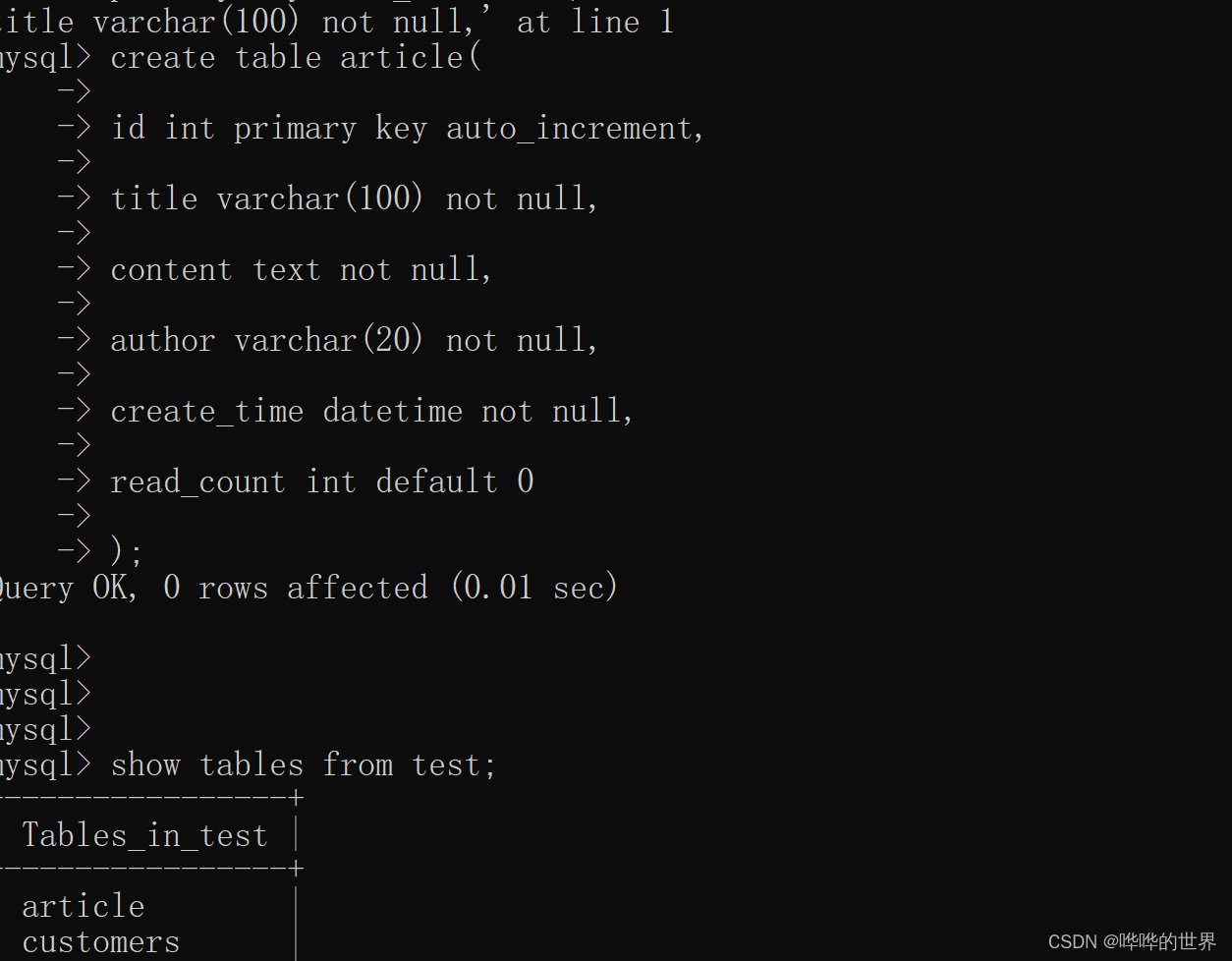
MySQL 表的基本操作,结合项目的表自动初始化来讲
有了数据库以后,我们就可以在数据库中对表进行增删改查了,这也就意味着,一名真正的 CRUD Boy 即将到来(😁)。 查表 查看当前数据库中所有的表,使用 show tables; 命令 由于当前数据库中还没有表,所以输出 Empty set。 不指定数据库 在操作表之前,可以通过 use 数据库名; 命令,指定要操作的数据库。 那假如不指定数据库的话,我们可以通过 sh
W3c泥垢!如此耿直。。。你是来讲冷笑话的吗?
学海无涯,且学且吐槽,W3C真是一个耿直的网站~~ 首先,强烈建议在学习属性之前标出浏览器支持选项,不然,就会在看完一大段说明之后,赫然发现: & 很好,谁来总结一张表,就叫:那些所有主流浏览器都不支持的html/CSS方法与属性。 顺便推荐网站http://caniuse.mojijs.com/Home/Html/item/key/css-touch-ac
职高学计算机语数英学的不好,对于中职生来讲,高职高考难吗?
原标题:对于中职生来讲,高职高考难吗? 高职高考难吗?这一个问题一直困扰着一些想要报考高职高考的同学,高职高考难度多多少少让他们望而却步。但我却认为高职高考不难也不容易。 “高职高考难吗?”实在是因人而异。首先我们要了解高职高考考什么知识!高职高考里包含有中考的内容和高中三年的语数英知识,如果你的基础很差,中考都拿不到三百分,高职高考对你来说难度就很大了,因为中考的内容都还没掌握好,比中考更上一
【2023年度总结与2024展望】---23年故事不长,且听我来讲
文章目录 前言一、学习方面1.1 攥写博客1.2 学习内容1.3 参加比赛获得证书 二、生活方面2.1写周报记录生活 三、运动方面四、CSDN的鼓励五、24年展望总结 前言 时光飞逝,又是新的一年,遥想去年2023年我也同样在这个时间段参加了CSDN举办的年度总结活动,那个时候的我青涩,懵懂,一边感受大学美好的校园,一边进入学校的ACM实验室学习算法,参加很多比赛,虽然结
对于区块链来讲,想要真正把新技术串联在一起
区块链,元宇宙的“开门之匙” 仅仅只是简单地将元宇宙与区块链划等号,其中一个很直接的结果就是将会混淆两者之间的主次地位。当越来越多的人将元宇宙与区块链深度联系,他们仅仅只是看到了元宇宙被资本市场和行业巨头们追捧的现实,并未真正明了区块链与元宇宙之间的内在联系。在很多情况下,区块链扮演的是元宇宙的“开门之匙”的角色和作用。 所谓的“开门之匙”,主要体现的是区块链的技术演进对于其他外在的技
java 反射机制:简单来讲,通过反射,类对我们是完全透明的,想要获取任何东西都可以。
什么是反射机制 在程序运行状态中,对于任意一个类或对象,都能够获取到这个类的所有属性和方法(包括私有属性和方法),这种动态获取信息以及动态调用对象方法的功能就称为反射机制。 简单来讲,通过反射,类对我们是完全透明的,想要获取任何东西都可以。 反射机制的优点 可以在程序运行过程中,操作这些对象;可以解耦,提高程序的可扩展性。 什么是反编译 反编译就是把*.class 文件逆向生成*.jav
从某种意义上来讲,数实融合,是产业互联网的一个表现
阿里加快步伐拥抱AI电商,腾讯在全真互联网的新征途上渐入佳境,京东持续精耕上游供应链,拼多多死磕三农不放松…… 这些现象的背后,是数实融合的大趋势。 当数实融合的步伐逐渐加快,特别是当越来越多的互联网玩家开始拥抱AI,开始将关注的焦点,聚焦在上游的产业端。 产业互联网的路径,正在变得比以往任何一个时候都要清晰。 从某种意义上来讲,数实融合,是产业互联网的一个表现。 以往,我们所认识的产业
从某种意义上来讲,数实融合,是产业互联网的一个表现
阿里加快步伐拥抱AI电商,腾讯在全真互联网的新征途上渐入佳境,京东持续精耕上游供应链,拼多多死磕三农不放松…… 这些现象的背后,是数实融合的大趋势。 当数实融合的步伐逐渐加快,特别是当越来越多的互联网玩家开始拥抱AI,开始将关注的焦点,聚焦在上游的产业端。 产业互联网的路径,正在变得比以往任何一个时候都要清晰。 从某种意义上来讲,数实融合,是产业互联网的一个表现。 以往,我们所认识的产业
C# 事实证明学好数学对编程来讲是多么重要
文章目录 背景协议补充说明如何用代码求解尝试穷举寻找规律经人指点得到良方 背景 做上位机开发时,上位机和下位机如何进行通讯,一般取决于下位机。有这样一个通信协议: 当上位机给下位机发送 19 02 01 时,代表读故障码当下位机响应 59 02 01 DD 时,代表肯定响应,其中 DD 代表故障码故障码用4个字节表示每一帧数据为8个字节当无故障码或仅有一个故障码时,一个数据帧
⟨A⟩ = Tr(ρA) 从数学上来讲什么意思
当给定一个具体的密度矩阵ρ和一个可观测量A时,我们可以通过数值计算来演示〈A〉 = Tr(ρA) 的应用。 假设我们有以下密度矩阵和可观测量: ρ = [0.6 0.3; 0.3 0.4] A = [1 0; 0 -1] 我们首先计算ρA的乘积: ρA = [0.6 0.3; 0.3 0.4] * [1 0; 0 -1] = [0.6 -0.3; 0.3 -0.4] 然后计算乘积的迹:
⟨A⟩ = Tr(ρA) 从数学上来讲什么意思
当给定一个具体的密度矩阵ρ和一个可观测量A时,我们可以通过数值计算来演示〈A〉 = Tr(ρA) 的应用。 假设我们有以下密度矩阵和可观测量: ρ = [0.6 0.3; 0.3 0.4] A = [1 0; 0 -1] 我们首先计算ρA的乘积: ρA = [0.6 0.3; 0.3 0.4] * [1 0; 0 -1] = [0.6 -0.3; 0.3 -0.4] 然后计算乘积的迹: