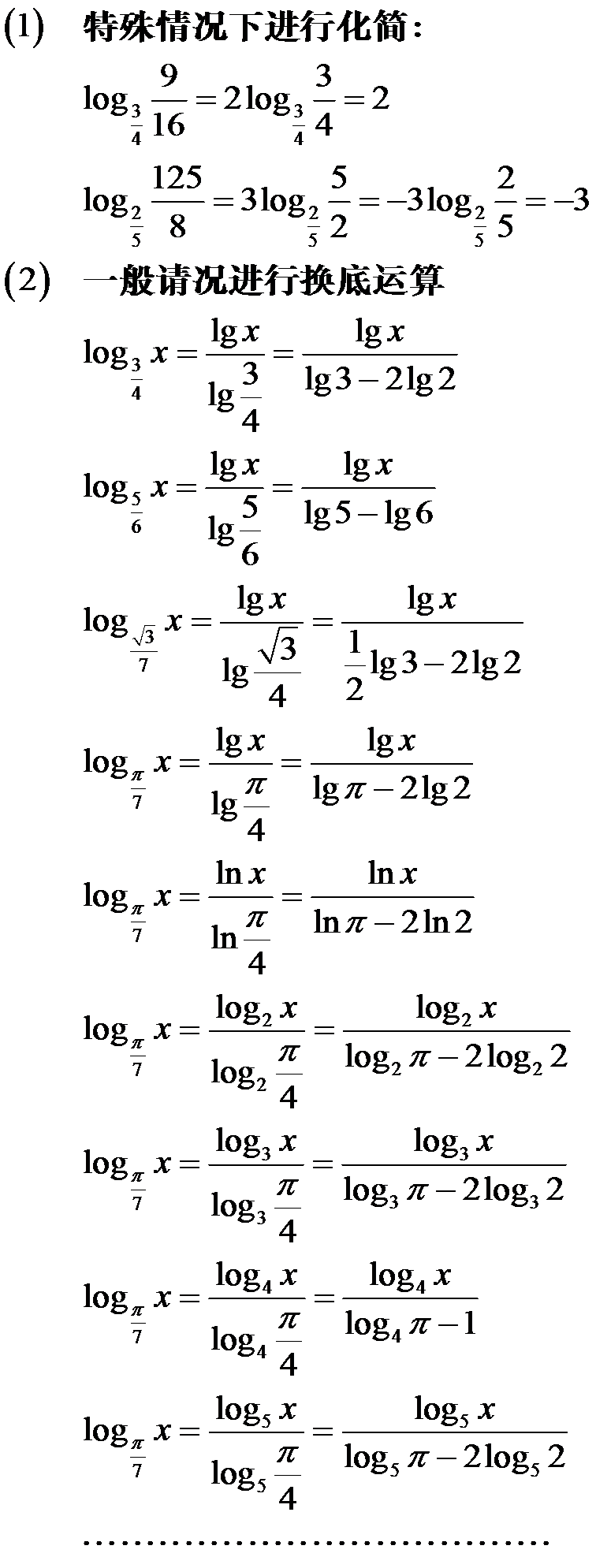推论专题

在DAG（有向无环图）上的常见推论

1.DAG上某条边可能被经过的次数数量：通过在DAG上的总结，再结合我们在小学学过的乘法原理，我们可以考虑到一个规律：在一条边M（u->v）上，通过M的方法数量为从源点到达u的方式数量*从终点到达v的方式数量. 2.DAG上某个点可能被经过的次数数量：使用DP，并配合拓扑排序即可。

TypeScript-类型推论和any类型

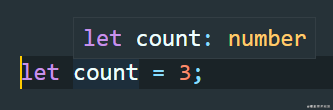
类型推论在TS中存在类型推断机制，在没有给变量添加类型注解的情况下，TS也会给变量提供类型 // 声明变量并赋值时let age = 18 // 推断为也是 number 类型 // 决定函数返回值时function add(a: number, b: number) {return a + b // 推断为也是 number 类型} let count = 100count

对数换底及常用推论

8. TypeScript 类型推论和类型断言

类型推论在TypeScript 中，有很多时间并不需要显式地指定变量的类型，TypeScript的一大优势是它的类型推论机制,可以自动推断变量、函数参数和返回值的类型,从而减少了手动类型注解的需求。变量类型推论 TypeScript 可以根据变量的初始值推断出变量的类型。例如: let x = 3; // x 被推断为 number 类型let y = "hello"; // y 被

TypeScript学习笔记（三）类型推论

1.什么是类型推论如果没有明确的指定类型，TypeScript 会依照类型推论（Type Inference）的规则推断出一个类型 let myFavoriteNumber = 'seven';myFavoriteNumber = 7;// index.ts(2,1): error TS2322: Type 'number' is not assignable to t

【TypeScript系列】类型推论

类型推论介绍这节介绍TypeScript里的类型推论。即，类型是在哪里如何被推断的。基础 TypeScript里，在有些没有明确指出类型的地方，类型推论会帮助提供类型。如下面的例子 let x = 3; 变量x的类型被推断为数字。这种推断发生在初始化变量和成员，设置默认参数值和决定函数返回值时。大多数情况下，类型推论是直截了当地。后面的小节，我们会浏览类型推论时的细微差

0008、ts的类型推论

TypeScript的类型推论是指在某些情况下无需明确指定变量的类型，TypeScript编译器会自动为其推断出一个类型。这是TypeScript提供的一项强大功能，能够让代码既简洁又具有类型安全性。接下来，我们将详细探讨类型推论的使用场景、应用技巧，并进行总结。使用场景变量初始化：当你初始化变量时，TypeScript会根据赋值给变量的值来推断其类型。函数返回值：当函数根据返回语句的值可

TypeScript 从入门到进阶之基础篇(六) 类型（断言、推论、别名）| 联合类型 | 交叉类型

系列文章目录 TypeScript 从入门到进阶系列 TypeScript 从入门到进阶之基础篇(一) ts基础类型篇TypeScript 从入门到进阶之基础篇(二) ts进阶类型篇TypeScript 从入门到进阶之基础篇(三) 元组类型篇TypeScript 从入门到进阶之基础篇(四) symbol类型篇TypeScript 从入门到进阶之基础篇(五) 枚举类型篇持续更新中…

Typescript 类型推论

TypeScript 会在没有明确的指定类型的时候推测出一个类型，这就是类型推论。如果没有明确的指定类型，那么 TypeScript 会依照类型推论（Type Inference）的规则推断出一个类型。以下代码虽然没有指定类型，但是会在编译的时候报错： let myFavoriteNumber = 'seven';myFavoriteNumber = 7;// index.ts(2,

TypeScript的类型推论与联合类型--(TypeScript 03)

什么是TS中的类型推断？以下面的例子为例，有时候我们并没有进行类型注解，TS经过推断后给我们添加的类型注解。什么时候需要进行类型注解什么时候不需要呢？比如下面的代码，TS能够推断的，我们可以不进行注解 let a = 3; 比如下面的代码，TS不能够对参数进行推断的情况下，我们需要进行注解 function test(a,b) {return a