布朗运动专题
分数布朗运动FBM期权定价模型
BS定价模型和蒙特卡洛模拟期权定价方法都 假设标的资产价格的对数服从布朗运动 . 但是实际 的金融市场中标的资产价格运动过程具有 “尖峰厚尾 ” 现象 , 运用分数布朗运动 (FBM )来刻画标的资产 价格的运动过程可能更加合适。 分数布朗运动属于高斯过程,它不再具备马尔 科夫性 , 但具有长程相依性 、 自相似性与 “ 尖峰厚尾 ” 等特性。 这些良好的性质使
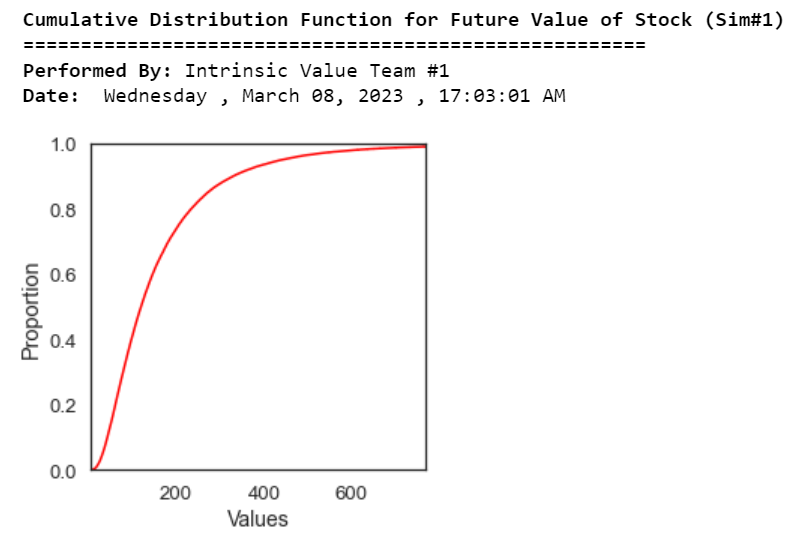
Python 中具有漂移的指数布朗运动;模拟股票价格的未来分布,以预测股票的未来价值
一、说明 随机过程是由概率定律生成的一系列事件或路径。也就是说,随机事件可以随着时间的推移而发生,但受特定的统计和概率规则的约束。主要的随机过程是随机游走或布朗运动。这个过程可以用来预测许多变量,这些变量似乎遵循随机趋势,但受到概率定律的限制。 图片来源:内在价值 二、赋予动机
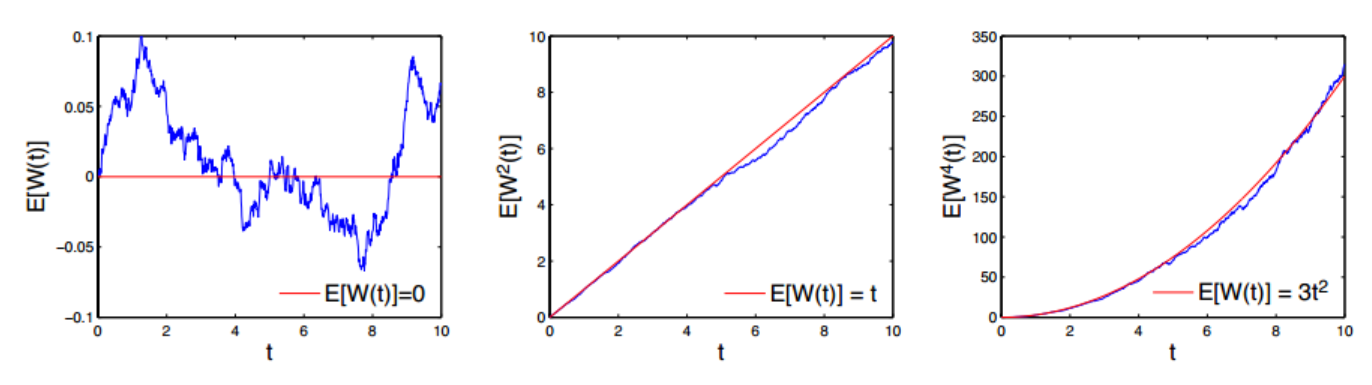
【随机过程】布朗运动
这里写目录标题 Brownian motion Brownian motion The brownian motion 1D and brownian motion 2D functions, written with the cumsum command and without for loops, are used to generate a one-dimensional