将军专题
将军百战死,程序十年成
将军百战死,程序十年成 十年前的 2014.8.3 我释出了动词算子式通用代码生成器的第一个完整版本 InfinityGPGenerator 0.6.5,即无垠式通用代码生成器 0.6.5。这是一个重大的里程碑。十年后,通用代码生成器已经是一个大家族。昨天,释出了 Golang 通用代码生成器仙童 2.4.0 电音仙女尝鲜版九。此版本支持完善的数据库自动反射功能。大大完善了数据与元数据编辑器功能
一致性hash理解、拜占庭将军问题解读和CAP理论总结
一致性hash理解 白话概述: 比如说存储图片,有10台服务器用来存储,对图片名进行hash(pic_name)%10得到的值就是图片存放的服务器序号。这是正常的hash算法分散图片存储。但是有一天,你觉得服务器不够了,需要加几台机器扩容存储。这时候,假设加了10台,变成20台,那么原先譬如11%10=1现在11%20=11,则存取图片会跑到11号服务器,如果仍旧用原来的算法,那所有图片几乎都要
分布式与一致性协议之拜占庭将军问题(一)
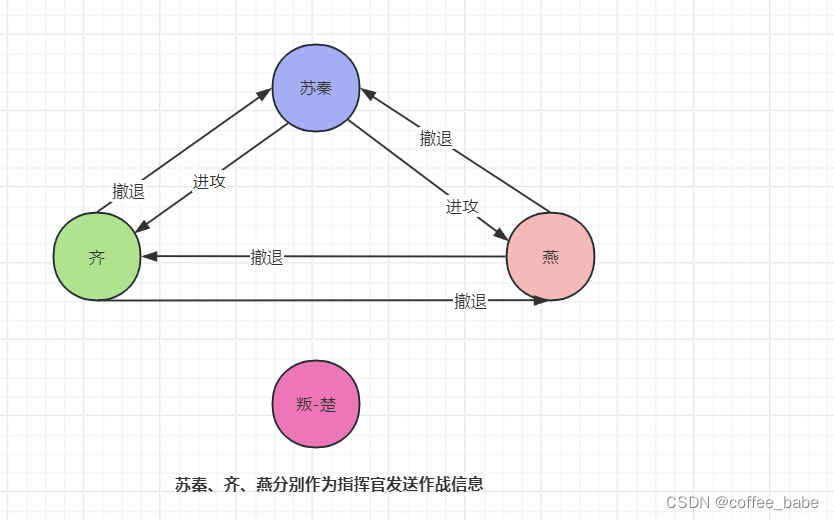
拜占庭将军问题 概述 拜占庭将军问题其实是借拜占庭将军故事展现了分布式共识问题,探讨和论证了解决的办法。实际上,拜占庭将军问题是分布式领域最复杂的一个容错模型,一旦搞懂了它,久能掌握分布式共识问题的解决思路,还能更深刻地理解常用的共识算法,这样在设计分布式系统的时候,就能根据场景特点,更好地选择或者设计合适的算法 什么是拜占庭将军问题? 以战国时期六国抗秦的故事为主线串联 苏秦的困境
分布式理论-拜占庭将军(译)
作者:LESLIE LAMPORT, ROBERT SHOSTAK, and MARSHALL 1982 译者:phylips@bmy 出处:http://duanple.blog.163.com/blog/static/7097176720112643946178/ [序:我一直觉得正是因为通过用一组围坐在圆桌旁的哲学家来表述,Dijkstra 的哲学家就餐问题才变得如此让人关注。(比如
拜占庭将军问题相关问题
1、拜占庭将军问题基本描述 问题 当我们讨论区块链共识时,为什么会讨论拜占庭将军问题? 区块链网络的本质是一个分布式系统,在存在恶意节点的情况下,希望整个系统当中的善良节点能够对于重要的信息达成一致,这个机制通常被称作共识机制(consensus)。 而上述问题的本质就是拜占庭将军问题。 解决方案区别 崩溃容错协议(CFT)和拜占庭容错协议(BFT)的区别 在分布式系统当中,依
学习区块链(十一)--从拜占庭将军问题谈谈为什么pow是最好的共识机制
这一节,不再去学习如何写代码,而是想聊聊共识机制,我们知道基于区块链技术现在有很多的共识机制,包括不限于POW,POS,DPOS,PBFT……,我先不说为什么我最认可POW,我们先来看看著名的拜占庭将军问题: 拜占庭帝国即中世纪的土耳其,拥有巨大的财富,周围10个邻邦垂诞已久,但拜占庭高墙耸立,固若金汤,没有一个单独的邻邦能够成功入侵。任何单个邻邦入侵的都会失败,同时也有可能自身被其他9个邻邦
NO.18 什么是拜占庭将军问题
本文是转载,转载自苏神的博客,原文地址:https://www.jianshu.com/p/5fea30b25f0a 拜占庭将军问题很多人可能听过,但不知道是什么意思,本文从非专业的角度来讲讲,拜占庭将军问题到底是说什么的。 拜占庭将军问题(Byzantine Generals Problem),首先由Leslie Lamport与另外两人在1982年提出,很简单的故事模型
3、漫谈分布式系统、拜占庭将军问题与区块链
分布式系统和一致性问题 拜占庭将军问题 我们前面讨论的一致性协议,有一个重要的前提条件,就是:各个节点都是可以信任的,它们都严格遵守同样的一套规则。这个条件,在一个公司的内部网络中可以认为是基本能满足的。但如果这个条件不满足会怎么样呢?假设网络中有些节点是恶意的,它们不但不遵守协议,还故意捣乱(比如胡乱发送消息),那么其它正常的节点还能够顺利工作吗? 在分布式系统理论中,这个问题被抽象成了一
断箭不相信自己的意志,永远也做不成将军。
断箭不相信自己的意志,永远也做不成将军。 春秋战国时代,一位父亲和他的儿子出征打战。父亲已做了将军,儿子还只是马前卒。又一阵号角吹响,战鼓雷鸣了,父亲庄严地托起一个箭囊,其中插着一只箭。父亲郑重对儿子说:“这是家袭宝箭,配带身边,力量无穷,但千万不可抽出来。” 那是一个极其精美的箭囊,厚牛皮打制,镶着幽幽泛光的铜边儿,再看露出的箭尾。一眼便能认定用上等的孔雀羽毛制作。儿子
2021内蒙古自治区第十六届“华讯杯”大学生程序设计竞赛---- 将军棋
这天Alice和Bob在玩一个经典的棋盘游戏——将军棋。 由于将军棋的规则比较复杂,他们决定玩简化版的将军棋,简化后的规则如下: 游戏开始在一个N*M的地图上,每个格子的位置由(x,y),x∈[1,N],y∈[1,M]表示。每个格子可以驻扎一些小兵。开始前Alice和Bob各占据一个格子,称为各自的城堡。城堡开始时有若干个小兵。初始时地图上除了各自的城堡所在的格子,都为空(即没有任何一方的小兵)
圆内接四边形周长最大_解读【第59、60题】“将军饮马”之四边形周长或面积最(小)大...
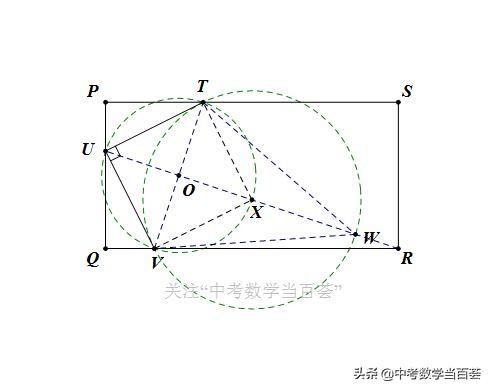
关注“中考数学当百荟”,感谢您的点赞,转发! 一.回顾“将军饮马”问题 图1 将军饮马问题 如图1所示,将军从巡视点M点出发,走到河边l饮马后再回到营地N点,请问怎样走才能使总的路程最短? 解决策略分两步 第一步 先找出这个点;第二步 再证明这个距离最短。 第一步 先找出这个点 利用轴对称(镜面反射),找点M关于直线l的对称点M’,连接M’N,M’N与l的交点O,即为所求,即此时
两军问题与拜占庭将军问题
下面这篇文章,感觉讲的非常好: http://www.8btc.com/baizhantingjiangjun 拜占庭将军问题是一个共识问题: 首先由Leslie Lamport与另外两人在1982年提出,被称为The Byzantine Generals Problem或者Byzantine Failure。核心描述是军中可能有叛徒,却要保证进攻一致,由此引申到计算领域,发展成
面试前准备好这些,Offer拿到手软,将军不打无准备的仗
《孙子兵法》有云:夫未战而庙算胜者,得算多也;未战而庙算不胜者,得算少也。多算胜,少算不胜,而况于无算乎!吾以此观之,胜负见矣。 由此可引申为面试提前作好准备,方能极大概率提升我们拿offer的成功率,下面来跟大家聊聊面试可能要问的那些高频问题,我们好对应做好准备! 一、问题预测 1. 让简单介绍下自己(每次面试开场) 2. 让说下自己会的内容 3. 看了哪些书籍(有问到)