圆上专题
2023第十四届蓝桥杯国赛C/C++ 大学 A 组 圆上的连线
思路：很显然总的方案数等于挑选偶数点的方案数乘以对应偶数点的连线方案数之和，挑选偶数点的方案数靠组合数得出，偶数点的连线方案数就是个卡特兰数。具体为什么是卡特兰数，可以任选一个点，枚举这个点所连边的位置，这条边把点分为两部分，方案数等于这俩小部分各自方案数的乘积，结合卡特兰数的性质， #include<bits/stdc++.h>using namespace std;#define i
![BZOJ 1041 [HAOI2008] 圆上的整点（数论）](/front/images/it_default2.jpg)
BZOJ 1041 [HAOI2008] 圆上的整点（数论）
Description 求一个给定的圆(x2+y2=r^2)，在圆周上有多少个点的坐标是整数。 Input 只有一个正整数n,n<=2000 000 000 Output 整点个数 Sample Input 4 Sample Output 4 Hint 科普视频 Source 太神了，竟然和素数扯上关系。 https://blog.csdn.net/csyzcyj/article/det
HHU 1015 圆上的点点点点点点点点点点点点点点（水题）
题意：假设圆的圆心位于(0,0)，半径为r，圆的"某积"公式为S=r2，请问"某积"为s的圆上有多少个以整数为坐标的点？ 思路：想办法优化双重循环就直接单重循环中间判断，但需要注意非0数开平方会有正负两个值，需要+2。 #include <iostream>#include <string.h>#include <algorithm>#include <math.h> using
UVA 11186 - Circum Triangle（圆上三角形求法）
这个题 感觉数据是500 就直接三层循环上去了。 。但是超时了。 我用了最简单的方法 可能是运算量略大的原因吧。（好吧。 在自己稍微优化之后A了。 跑了2.059秒，代码在最后面） 在不会优化的情况下。 去网上搜了题解。 第一份代码。 在我看明白之后 不得不佩服 原作者的聪明机智。 也算是 学到了。 先上代码后讲解。 #include <cs
SCAU:判断点是否在圆上
判断点是否在圆上 Time Limit:1000MS Memory Limit:65536K 题型: 编程题 语言: G++;GCC 描述 由键盘输入一个点的坐标, 要求编程判断这个点是否在单位圆(圆心在坐标0,0)上，点在圆上输出Y, 不在圆上输出N。使用小数点后3位精度进行判断。 输入样例 0.707,0.707 输出样例 Y #include <stdi
SCAU:判断点是否在圆上
判断点是否在圆上 Time Limit:1000MS Memory Limit:65536K 题型: 编程题 语言: G++;GCC 描述 由键盘输入一个点的坐标, 要求编程判断这个点是否在单位圆(圆心在坐标0,0)上，点在圆上输出Y, 不在圆上输出N。使用小数点后3位精度进行判断。 输入样例 0.707,0.707 输出样例 Y #include <stdi
易懂的Bresenham算法计算圆上各点坐标
Bresenham简介： 在我们内部开发使用的一个工具中，我们需要几乎从 0 开始实现一个高效的二维图像渲染引擎。比较幸运的是，我们只需要画直线、圆以及矩形，其中比较复杂的是画直线和圆。画直线和圆已经有非常多的成熟的算法了，我们用的是Bresenham的算法。 计算机是如何画直线的？简单来说，如下图所示，真实的直线是连续的，但我们的计算机显示的精度有限，不可能真正显示连续的直线，于是我们用一系
RationalDMIS 2020一平面与两偏置圆找正（原点不在偏置圆上）
如图所示，该零件的特点是两找正孔的连线与坐标轴线不平行，且为间接原点设置。 显然，按常规方法很难找正。 考虑到该类产品在实际测量中并不少见，所以，我们根据图样设计要求，选择了既方便操作又便于推广的最佳拟合坐标系的方法，应用效果非常满意。 具体操作步骤如下： 1.测平面，找正零件坐标系的第一轴；质心置零点 MODE/MANF(PLN1)=FEAT/PLANE,CAR
RationalDMIS 2020 一平面与两偏置圆找正（原点在一偏置圆上）
如图所示，该零件的第1轴是通过测量一个平面来找正的，面质心点置原点；第2轴由于两圆连线不平行于坐标轴，所以，从传统的概念上，不少用户都是通过图样给定的两孔理论坐标值，计算出一个理论坐标轴的旋转角度，来完成坐标系找正的。事实上这种方法不仅麻烦，找正的效果也有一定的局限性。 具体操作步骤如下： 1.测平面1，找正零件坐标系的第一轴。质心置零点。 MODE/MANF(PL
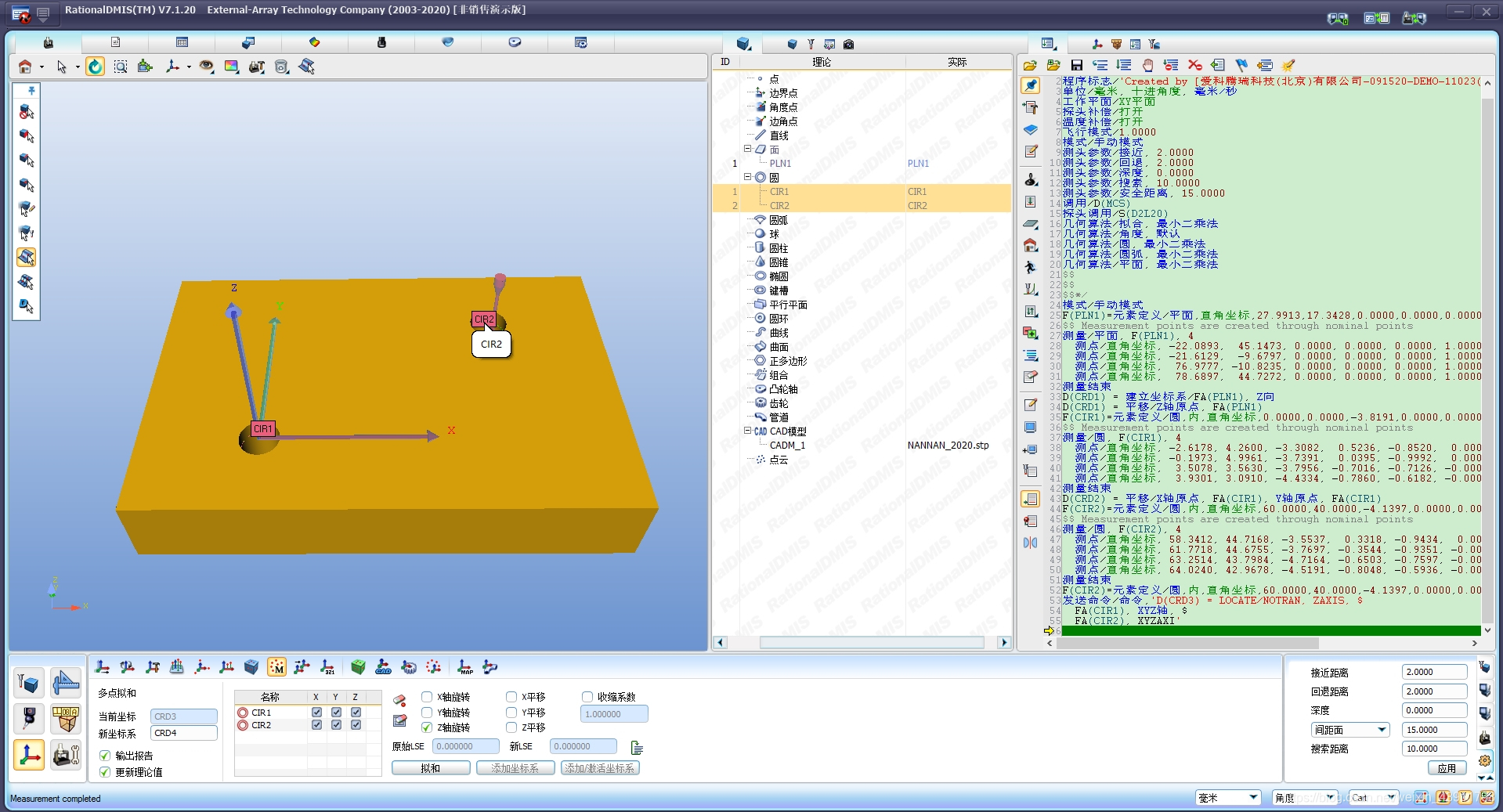
RationalDMIS 7.1 一平面与两偏置圆找正（原点在一偏置圆上）
如图所示，该零件的第1轴是通过测量-一个平面来找正的，面质心点置原点；第2轴由于两圆连线不平行于坐标轴，所以，从传统的概念上，不少用户都是通过图样给定的两孔理论坐标值，计算出一个理论坐标轴的旋转角度，来完成坐标系找正的。事实上这种方法不仅麻烦，找正的效果也有一定的局限性。 *具体操作步骤如下： 1.测平面1，找正零件坐标系的第一轴； 2.测圆1，圆心置原点； 3.测圆2并按图样进行（2D）理
RationalDMIS 7.1-平面与两偏置圆找正（原点不在偏置圆上）
如图所示，该零件的特点是两找正孔的连线与坐标轴线不平行，且为间接原点设置。显然，按常规方法很难找正。 考虑到该类产品在实际测量中并不少见，所以，我们根据图样设计要求，选择了既方便操作又便于推广的最佳拟合坐标系的方法，应用效果非常满意。 *具体操作步骤如下： 1.测平面，找正零件坐标系的第一轴； 2.测圆1和圆2；按图样对圆1和圆2进行（2D）理论坐标值的修改； 3.选圆1、圆2平移和旋转完