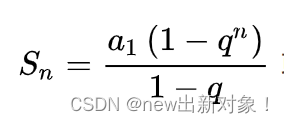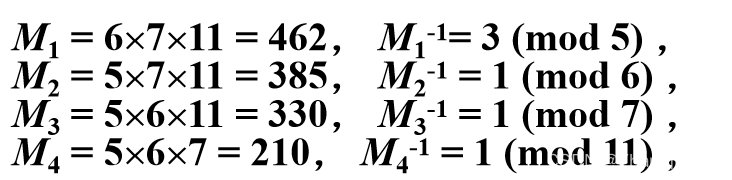同余式 同余式是 数论 的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m| (a-b)，则称a与b对模m 同余 ，记为a≡b (mod m)，或记为a≡b (m)。 这个式子称为模m的同余式，若m∤ (a-b)，则称a、b对模m不同余 同余概念又常表达为： 1.a=b+km (k∈Z)； 2.a和b被m除时有相同的 余数  乘法逆元 乘法逆元的定义：在数学领域，对于群G

6.1 剩余系（掌握） 6.2 同余式概念与一次同余式（熟练） 6.3 中国剩余定理（熟练） 6.1 剩余系 设m是正整数，模m同余的全体整数是一个模m剩余类，即可表示为a = qm+r， 0≤r<m，q=0，±1，±2，…，  的整数是一个模m剩余类。 剩余类中的每个数都称为该类的代表 r称为该类的最小非负剩余 模m剩余类共有m个 例：全部模8的剩余类为 {0，±8，±2×8，±3×8，