题意：Maximum Sum 的加强版，多了个可以构成环，那么就把图扩大成4倍，然后枚举每种情况 #include <iostream>#include <cstdio>#include <cstring>using namespace std;const int MAXN = 210;int a[MAXN][MAXN],b[MAXN];int main(){int n,t;sca

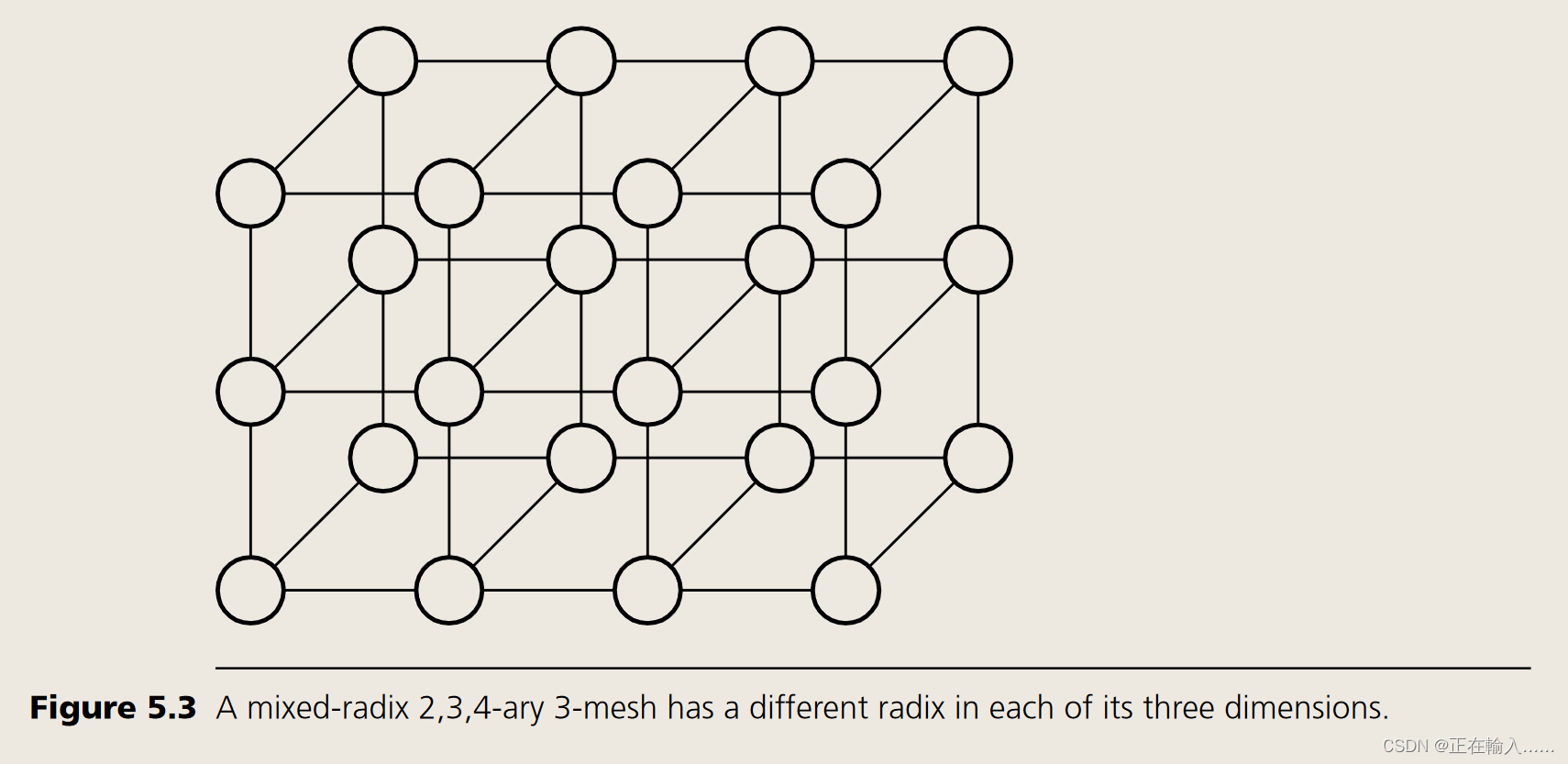
1. Torus 网络拓扑2. Torus 网络拓扑结构References 1. Torus 网络拓扑 Torus 和 Mesh 网络拓扑，又可以称为 k-ary n-cubes，在规则的 n 维网格中包裹着 N = k^n 个节点，每个维度都有 k 个节点，并且最近邻居之间有通道。k-ary n-cubes包含一系列网络，从 rings (n = 1) 到 binary n-cubes (

和108题意差不多。 就是这个题的原始数据不是存在矩阵里面。而是存在环图中。 什么叫做环图呢，就是对于n*n的矩阵，若某个时间走到最后一列，再次向右走的话，此时会走到第一列，就好像是滚动数组一样。 思路很108一样，只不过把为了满足环图的特点。我们需要把图放大4倍。。 代码如下： #include <cstdio>#define M 330int n, a[M][M];int