solutions专题
ultralytics solutions快速解决方案,快速实现某些场景的图像解决方案
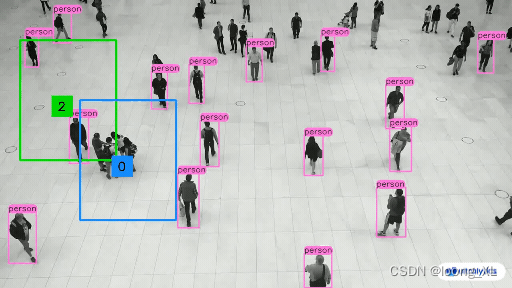
参考: https://docs.ultralytics.com/solutions/ 在不断更新,已经有一些场景的解决方案 ultralytics 8.2.27 一、区域统计 1、自定义区域统计数量 https://docs.ultralytics.com/guides/region-counting/ 1、自定义画框,比如矩形框四个点的坐标获取 通过cv2点击图片获取像素点坐
uva 11020 - Efficient Solutions(STL)
题目链接:uva 11020 - Efficient Solutions 题目大意:依次给定n个人的坐标,每次输出当前有多少个人属于优势群体,优势群体的定义为不存在另一个人的坐标x,y均小于自己(等于是可以的)
UVA 11020 - Efficient Solutions(set)
UVA 11020 - Efficient Solutions 题目链接 题意:每个人有两个属性值(x, y),对于每一个人(x,y)而言,当有另一个人(x', y'),如果他们的属性值满足x' < x, y' <= y或x' <= x, y' < y的话,这个人会失去优势,每次添加一个人,并输出当前优势人个数 思路:由于每个人失去优势后,不可能再得到优势,所以失去优势就可以当成删去
利用脚本的导出结果及MATLAB结果分析偏振转换效率计算那些方向用到(FDTD Solutions)
在计算偏振转换效率时,通常需要考虑多个方向上的偏振态变化。偏振转换效率是衡量入射光的偏振态在通过某个系统或介质后发生变化的能力。这通常涉及到对光场的幅度和相位变化的详细分析。 如果你正在使用脚本(例如Python、MATLAB或其他语言)来处理FDTD模拟的导出结果,并希望分析偏振转换效率,那么你需要关注以下方面: 入射光的偏振态:首先,你需要知道入射光的偏振态。这可以是线偏振、圆偏振或椭圆偏
Internet Strategy: The Road to Web Services Solutions
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp Internet Strategy: The Road to Web Services Solutions reminds readers that several attempts have been m
Developing WMI Solutions: A Guide to Windows Management Instrumentation
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp This book helps developers and system administrators understand Windows Management Instrumentation (WMI).
Web Standards Solutions: The Markup and Style Handbook
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp This book is your essential guide to understanding the advantages you can bring to your web pages by im
.NET Development Security Solutions
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp The .NET Framework offers new, more effective ways to secure your Web and LAN-based applications. .NET
PC Magazine Windows Vista Security Solutions
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp When you want to defend Windows Vista,it's good to know a PC Magazine expert Unless a time machine jus
Pro EDI in BizTalk Server 2006 R2: Electronic Document Interchange Solutions
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp EDI is one of the next big waves in connected systems, as business becomes more dependent on working wi
The Real MCTS/MCITP Exam 70-620 Prep Kit: Independent and Complete Self-Paced Solutions
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp This exam is designed to validate proficieny supporting Windows Vista client. This exam will fulfill th
2022 Solutions Day成功举办
本月18日,银斯微在韩国首尔Yeouido Conrad Hotel举办了"2022 Solutions Day"。以"Ride the B.I.G.Waves(Beyond Web,Integrate IT,to the Gateway)"为主题,由于新冠疫情的影响,时隔3年,对公司的最新技术革新与产品功能迭代内容向客户与合作伙伴做了介绍。 ●Sessions ①【W
Solutions_to_Introduction_to_Algorithm_3nd_Exercise_4
4.1-1 What does FIND-MAXIMUM-SUBARRAY return when all elements of A are negative? The biggest negative one. 4.1-2 Write pseudocode for the brute-force method of solving the maximum-subarray problem.
Solutions_to_Introduction_to_Algorithm_3nd_Exercise_3
3.1-1 Let f(n) and g(n) be asymptotically nonnegative functions. Using the basic definition of Θ-notation, prove that max(f(n),g(n))=Θ(f(n)+g(n)). Let f(n),g(n) be asymptotically nonnegative. Show t
Introductory Combinatorics 5th Solutions Chapter1 7~13
Richard A.Brualdi 组合数学5th 课后习题答案 其实这篇文章只是用来记录我解题思路的笔记。 第一章 什么是组合数学 7.题目略 step1:若a即是m的因子也是n的因子,即必然存在k使: k x a = m ,k x a = n 成立,此时看b是m还是n的因子,若b为m的因子,则必然找到 j 使 j x b = m , 即可以用 j 个a x b 的牌组成 a x m 的
Android Studio Project Errors Solutions
1、Error:Execution failed for task compileReleaseRenderscript llvm-rs-cc is missing 错误原因:使用的SDK版本不匹配(SDK版本太低)。 参考:https://blog.csdn.net/fuchaosz/article/details/51483528 2、Android Studio3.0需要Gradle
Problems Solutions -- 9 No Socket could be created
这几天重新学习 Learn Python The Hard Way , 花了5~6 天时间,前前后后又学了一遍,收获很多。 遇到了这个错误: (learn_web) for-python@ubuntu:~/mystuff/projects/gothonweb$ python2 bin/app.pyhttp://0.0.0.0:8080/Traceback (most recent ca
Problems Solutions -- 9 No Socket could be created
这几天重新学习 Learn Python The Hard Way , 花了5~6 天时间,前前后后又学了一遍,收获很多。 遇到了这个错误: (learn_web) for-python@ubuntu:~/mystuff/projects/gothonweb$ python2 bin/app.pyhttp://0.0.0.0:8080/Traceback (most recent ca
Problems Solutions --8 SMTP in flask_mail
明明按照书中的代码来写,还是出错,大半天了。 还好解决了问题。 这样的报错 :smtplib.SMTPAuthenticationError: (535, b'Error: authentication failed') 解决办法竟然很简单: smtp 简单邮件传输协议。 然后,一般邮箱中这个服务是关闭的。 可以自己开启这个服务,以QQ邮箱为例,设置→账户设置→开启这个SMTP
Problems Solutions --8 SMTP in flask_mail
明明按照书中的代码来写,还是出错,大半天了。 还好解决了问题。 这样的报错 :smtplib.SMTPAuthenticationError: (535, b'Error: authentication failed') 解决办法竟然很简单: smtp 简单邮件传输协议。 然后,一般邮箱中这个服务是关闭的。 可以自己开启这个服务,以QQ邮箱为例,设置→账户设置→开启这个SMTP
Exercises and Solutions of Chapter 1
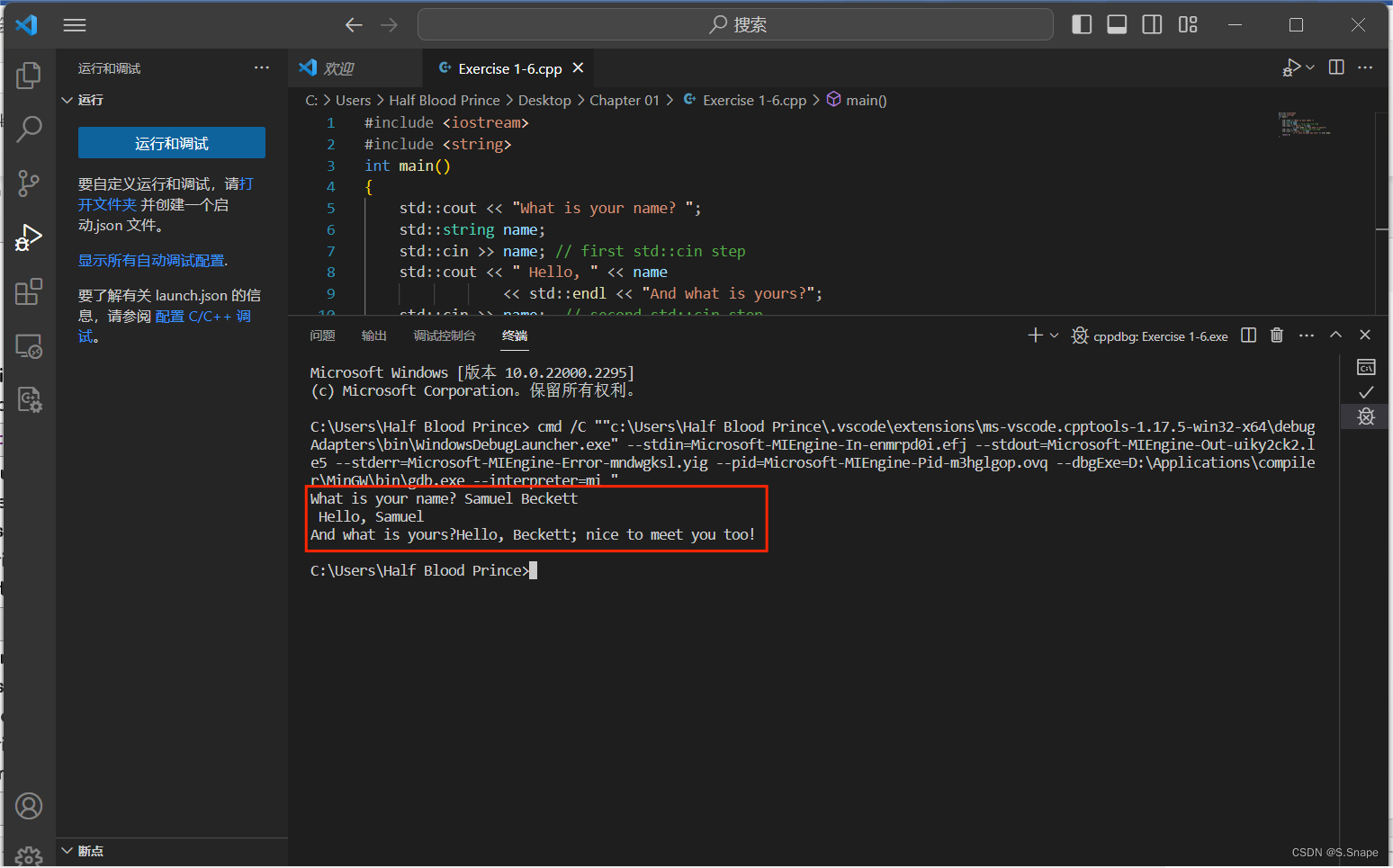
Exercise 1-0——Test chapter programsExercise 1-1——Understanding string concatenationExercise 1-2——Understanding string concatenationExercise 1-3——Understanding scopeExercise 1-4——Understanding scopeExe
使用matplotlib画3d平面风场_SLM Solutions上市12激光、20倍速NXG XII 600金属3D打印机_搜狐汽车...
昨日,SLM Solutions 12激光金属3D打印机正式发布,型号命名为NXG XII 600。这台备受期待的设备配备了12台1千瓦的激光器和600x600x600mm的成型舱室。NXG XII 600是目前市场上打印效率最快的设备,比SLM ®280单激光设备快20倍,同时使用光学变焦等创新技术,使其能够达到最佳的生产效率和稳定性。此设备主要用于大尺寸零件的批量化生产,为汽车和航空航
Document Solutions for Word(GcWord)6.2.5 Crack
GcWord Feature-Rich Microsoft Word Document API Library for .NET 6+ Document Solutions for Word (DsWord, previously GcWord) allows you to generate Word documents with speed, memory efficiency with no
some kernel panic reasons and solutions
Kernel Panic常见原因以及解决方法 Technorati 标签: Kernel Panic 出现原因 1. Linux在中断处理程序中,它不处于任何一个进程上下文,如果使用可能睡眠的函数,则系统调度会被破坏,导致kernel panic。因此,在中断处理程序中,是不能使用有可能导致睡眠的函数(例如信号量等)。 在中断发起的软中断中,其上下文环境有可能是中断上下文,
07 MIT线性代数-求解Ax=0:主变量,特解 pivot variables, special solutions
前面定义了矩阵的列空间和零空间,那么如何求得这些子空间呢? 1. 计算零空间 Nullspace A的零空间即满足Ax=0的所有x构成的向量空间 对于矩阵A进行“行操作”并不会改变Ax=b的解,因此也不会改变零空间 unchanged 第一步消元: echelon 阶梯型 pivot columns and free columns rank of A = # of piv