singular专题
Singular Value Decomposition:奇异值分解(降维)
SVD 降维 相似度计算: 1.欧式距离 向量的范数2 2.皮尔逊相关系数 cov(X,Y)varxvary c o v ( X , Y ) v a r x v a r y \frac{cov_{(X,Y)}}{var{x} var{y}} 均值意义:样本集合的中间点 方差意义: 样本点的离散程度 协方差意义: 度量两个随机变量关系的统计量 度量各个维度偏离其均值的程度 协方差计
[Flutter]导入singular_flutter_sdk后运行到Android报错
问题: 接入归因之前,flutter项目一起正常。接入归因之后,iOS正常Android有问题。 dependencies: # Singular归因singular_flutter_sdk: ^1.3.3 针对 Flutter 的 Singular SDK 集成指南 https://support.singular.net/hc/zh-cn/articles/4408894547227
Lombok:@Singular集合元素灵活添加利器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 一、@Singular介绍 二、使用示例 三、注意事项 四、使用场景 总结 提示:以下是本篇文章正文内容,下面案例可供参考 一、@Singular介绍 @Singular注解可以用在集合类型的字段上,它会生成两个方法,一个是添加单个元素的方法,一个是添加整个集合的方法。这两个方法可以和 @Build
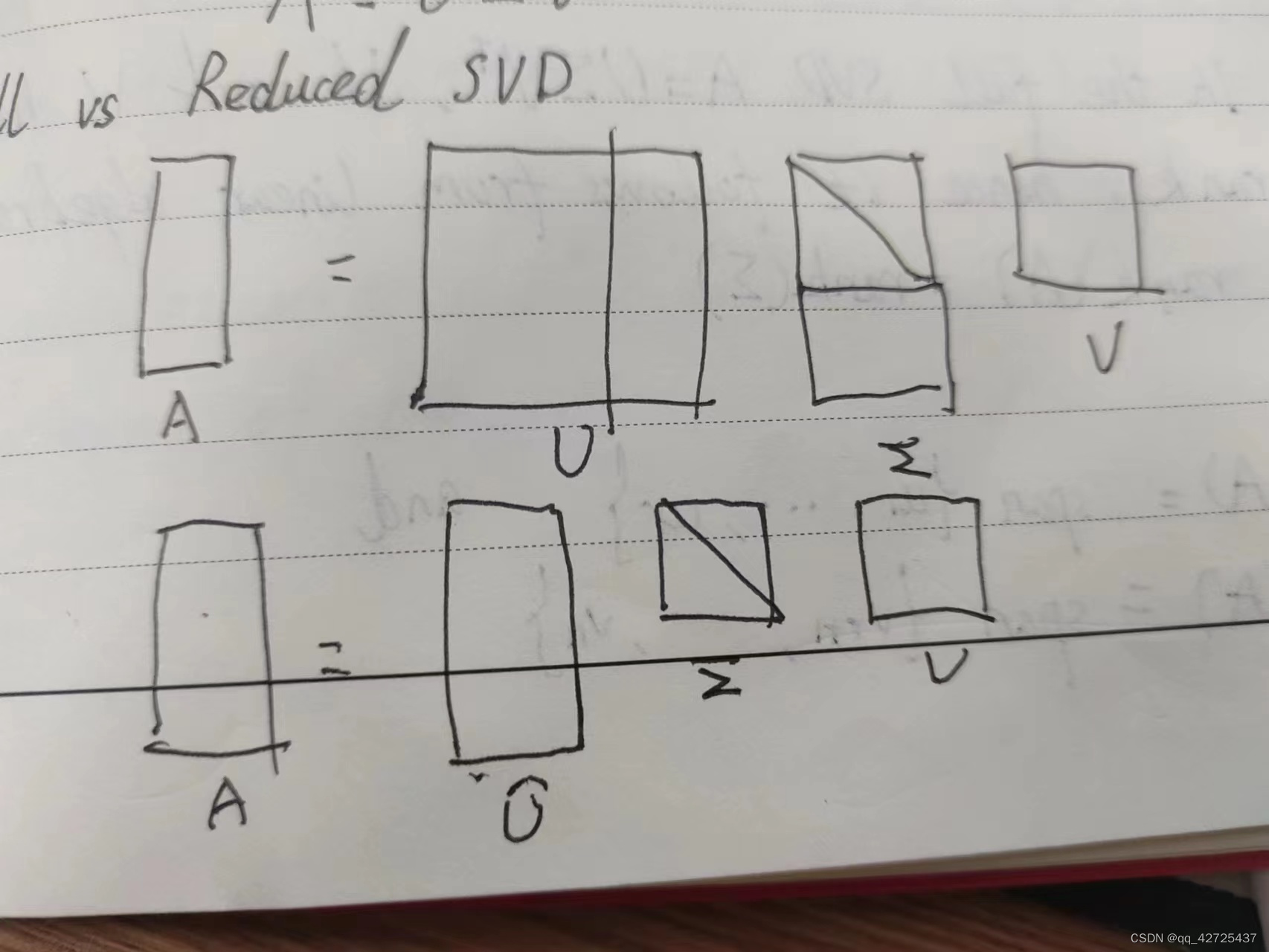
奇异值分解SVD(singular value decomposition)
奇异值分解 SVD是一个很有用的矩阵因子化方法。 SVD提出的目的:任何一个 m × n m\times n m×n的矩阵都可以当作一个超椭圆(高维空间的椭圆),可以把它们当作单位球体S的像。 一个超椭圆可以通过将单位球型在正交方向 u 1 , u 2 , . . . , u m \mathbf{u_1},\mathbf{u_2},...,\mathbf{u_m} u1,u2,...,um
R 语言【ashr】warning: solve(): system is singular (rcond:****); attempting approx solution
最近更新了R,升级到了4.2,在使用 ashr 对DESeq2结果进行 LFC shrinkage 的时候,突然出现了warning…… warning: solve(): system is singular (rcond: 2.12669e-17); attempting approx solution warning……其实不管它,对我最后的结果也不会有影响,但是,看着难受啊,忍不了…

![[Flutter]导入singular_flutter_sdk后运行到Android报错](/front/images/it_default.gif)