section专题
USACO Section 3.1 Humble Numbers
题意: 已知一个集合S 由S的任意子集作为因子 可构造出一个数字 求 这些构造出的数字中第k大的数字是多少 思路: 拿到这题就被“数字不是很多而且比较连续暴力枚举就好”这个思路迷惑了 果断TLE… 跪了一次后想到通过bfs构造可取 这时用了queue维护bfs 用priority_queue维护答案(大顶堆 内部最多k个数字) 用set判重复(5*2=2*5) 写
USACO Section 2.3 Fractions to Decimals
题意: 已知分子分母 求 该数字的小数形式 要求如果是循环小数用()表示出循环节 思路: 不循环小数容易处理 循环小数需要找出哪里是循环节 想象笔算除法的方法可以知道 当被除数的状态再次出现 则表示进入循环 用此方法即可 记录状态时候数组开的大点(我还用了map来映射该状态对应的位置) 因为循环节不一定什么时候出现… 我不会算… 注意: USACO对空格
USACO Section 2.3 Cow Pedigrees
题意: N个节点 深度为K 的正则二叉树 求 树有几种形态 思路: 一开始以为是数学题… 看了byvoid的题解才知道是dp… 每棵树由根节点、左子树、右子树构成 由此得状态转移 树=左子树*右子树 节点数和深度是影响答案的属性 所以令dp[i][j]表示i个节点深度在j以内的树的形态数 深度在j以内的树又两个深度在j-1以内的树和一个根节点构成 设左子树k个节
USACO Section 2.3 Longest Prefix
题意: 给你一大堆小字符串 和 一个大字符串 求 使用小字符串能拼出的大字符串的前缀最长是多少 思路: 由于数据不大 所以可以尝试扫描大字符串 每到一个位置用小字符串拼一下看看能拼多长 拼的最远距离就是答案 我用trie树来存小字符串集合 扫描大字符串时 如果该位置是可以向后延伸的(即之前能拼到这个位置) 那么我用一个标记在trie树上爬 每次发现一个小字符串结
USACO Section 1.5 Checker Challenge
题意: N皇后问题 输出 字典序最小的3种解法 和 解的数量 思路: dfs去放皇后判断和前面的皇后是否冲突 题目时间卡的超级很近!! 简单的搜索一定跪 能剪的地方要拼命剪枝!! 列举我的剪枝: 1.直接按字典序搜索 最先搜到的3个解保证字典序最小 直接输出 2.通过上几行皇后的放法 求出现在这行有几个位置能放皇后 之后进行搜索(这是关键!! 千万不要先搜位置
USACO Section 1.5 Prime Palindromes
题意: 输入a和b 求 a和b之间所有既是素数同时又有回文性质的数 从小到大输出 思路: 如果枚举a到b之间所有的数再判断素数和回文那么复杂度会比O(n)还大 本题O(n)都会跪 因此思路转到能否 先得到所有素数再判断回文 或者 先得到所有回文的数在判断素数 本题我的做法是后者 说下原因 本题b最大为10^8 因此构造回文的数字可以枚举1~10000中的数字再对数字翻折
USACO Section 1.4 Packing Rectangles
题意: 已知4个矩形的l和w 矩形可以旋转和平移 用一块最小面积的新的矩形覆盖4个矩形 求最小的面积 以及新矩形的l和w 思路: 题目已经给出6种摆放方式 按它的方式摆即可 我们要枚举4个矩形是否旋转(只转90度)过 然后枚举每种摆放方式中矩形的编号 代码中的枚举方法是二进制枚举旋转 全排列枚举编号 最后计算所有情况中的答案 第6种摆放方式比较难想 大致思路就是
双11GRE计划逻辑写作之Analytical Writing Section简介
双11还在刷屏购物吗,抽空和GRE频道一起来看看Analytical Writing Section简介: 逻辑写作是General GRE Test考试的三个必考部分之一,它的前身是ETS设计的写作单项考试AWA(Analytical Writing Assessment。ETS从02年10月份开始,正式将写作单项考试并入GRE考试,取代原有的GRE逻辑部分(Analytical Se
P1182 数列分段`Section II`
题目地址 个人思路: 显然是二分,但是有几个点要注意.左边界l需要初始化为数列中的最大值,否则就要在judge方法中进行繁琐的判断m是分成的段数,实际只能分m-1次洛谷的评测机不会给变量自动赋值,需要手动初始化l,r #include<cstdio>#include<iostream>using namespace std;const int MAXN=1000010,IN
configparser.DuplicateSectionError: While reading from '/home/qinghua/.theanorc' [line 18]: section
python代码: import theano 出现错误: configparser.DuplicateSectionError: While reading from '/home/qinghua/.theanorc' [line 18]: section 'nvcc' already exists 解决方法是, vim ~/.theeanorc 删除行: [nvcc]
Error Loading extension section usr_cert
在用easy_rsa生成ovpn配置时,出现如下错误: [ root: /usr/share/easy-rsa] #/usr/share/easy-rsa/build-key --batch zzzz.29761Using Common Name: zzzz.29761Generating a 2048 bit RSA private key...............+++.....
tableView section随cell移动 ,不在顶到屏幕顶部
加上这段代码即可 func scrollViewDidScroll(scrollView:UIScrollView) { let sectionHeaderHeight:CGFloat = 55 if scrollView.contentOffset.y <= sectionHeaderHeight && scrollView.con
解决unrecognized relocation (0x2a) in section `.text`
解决unrecognized relocation (0x2a) in section .text 问题: /usr/bin/ld: …/deps/zw/lib/libdmsdk.a(http.o): unrecognized relocation (0x2a) in section `.text’ /usr/bin/ld: final link failed: 错误的值 collect2:
goland 调试 could not launch process: decoding dwarf section info at offset 0x0: too short
Mac环境下,(其他环境类似) 1、错误信息: could not launch process: decoding dwarf section info at offset 0x0: too short 2、主要原因是: Mac环境下,go的版本比较新。 而goland使用的调试插件的版本低,导致的。 3、解决措施: 解决方案之一:对goland的调试插件进行升级。 3.1、下载、
ios 解决bug---UITableView删除到最后一个unable to generate a new section map with old section count: 1 and new
在iOS的UItableview删除中,删除操作我们经常用这样的语句 - (void)tableView:(UITableView *)tableView commitEditingStyle:(UITableViewCellEditingStyle)editingStyle forRowAtIndexPath:(NSIndexPath *)indexPath {if (editingStyle
No manual entry for XXX in section 3
centos 7 minimal安装下缺少man-page解决办法: #安装manyum install -y man#安装man-pageyum install -y man-pages
Fatal error: Please read Security section of the manual to find out how to run mysqld as root
原因: 这是因为在测试的时候,使用root来启动的。而从安全角度来讲,不建议用root用户启动。 解决方案: /usr/sbin/mysqld --skip-grant-tables --skip-networking --user=root &
iOS安全:静态混淆【Static obfuscation】1、使用宏进行替换字符串2、解析mach-o中对应的section进行类名和方法名的替换
文章目录 前言I、使用宏进行替换字符串II、二进制文件修改see also 前言 1.对抗hopper和ida的分析可以修改macho文件的某些偏移量, 让hopper和ida无法分析造成闪退 2.对抗class-dump 和工具分析可以方法名类名混淆,混淆方案大致三种 1)编译前用脚本批量做宏定义替换(最原始的方案:字符串替换) 2)LLVM混淆 逻辑混淆(花指令) 3)对
iOS小技能: tableView section间距失效的解决方案
文章目录 前言I section相关1.1 section的间距失效的解决方案1.2 修改 SectionHeader 字体及背景色1.3 自定义FooterView II 为UITableViewCell设置预估高度III 自定义cell样式3.1 显示Checkmark样式3.2 案例: 商品类目选择视图 前言 tableView 一些常用的细节技巧: tableView
iOS App thinning【( 通过 LinkMap、mach-o寻找优化点)】1、段迁移rename_section减小__TEXT 段大小(需关闭 Bitcode)2、查无用方法/类/宏/图
文章目录 前言I 、App thinning的实现方法:1.0 背景知识1.0.1 下载大小限制(ipa)1.0.2 可执行文件大小限制1.0.3 Mach-O1.0.4 Link Map File1.0.5 llvm-otool1.0.6 大、小端1.0.7 Runtime 1.1.Slicing1.2.Bitcode1.3.On-Demand Resources
子容器启动失败See section 8.2.2 2c of the Servlet specification for details. Consider using absolute orderi
子容器启动失败See section 8.2.2 2c of the Servlet specification for details. Consider using absolute ordering. 如果出现这种错误 找到项目的web.xml文件,然后在 <display-name>xxxxxxx</display-name> 标签下加一句代码,如下 <absolute-orde
MFC线程(二):线程同步临界区CRITICAL SECTION
当多个线程同时使用相同的资源时,由于是并发执行,不能保证先后顺序.所以假如时一个公共变量被几个线程同时使用会造成该变量值的混乱. 下面来举个简单例子. 假如有一个字符数组变量 char g_charArray[4]; CString szResult; AfxBeginThread(FunOne,NULL); //FunOne给数组赋值全为S AfxBeginThread(FunTw
【ARM64 常见汇编指令学习 14.1 -- ARM 汇编 .align 和 .section】
文章目录 ARM 汇编 .align 和 .section.align.section示例 ARM 汇编 .align 和 .section 在ARM64(或称为AArch64)汇编语言中,.align 和 .section 是两个常用的指令,它们在代码中扮演着重要的角色,尤其是在控制内存对齐和段(section)定义时。 .align .align 指令用于确保接下来的
C++ 关键段(Critical Section)CS深入浅出 之多线程(七)
CS我为什么要引入CRITICAL_SECTION和临界区呢?因为临界区是CRITICAL_SECTION的本质理论。 CS概述: 关键段(Critical Section)是一小段代码,它在执行之前需要独占对一些共享资源的访问权。这种方式可以让多行代码以“原子方式”对资源进行操控。这里的原子方式,指的是代码知道除了当前线程之外,没有其他任何线程会同时访问该资源。当然,系统仍然可以暂停当前线
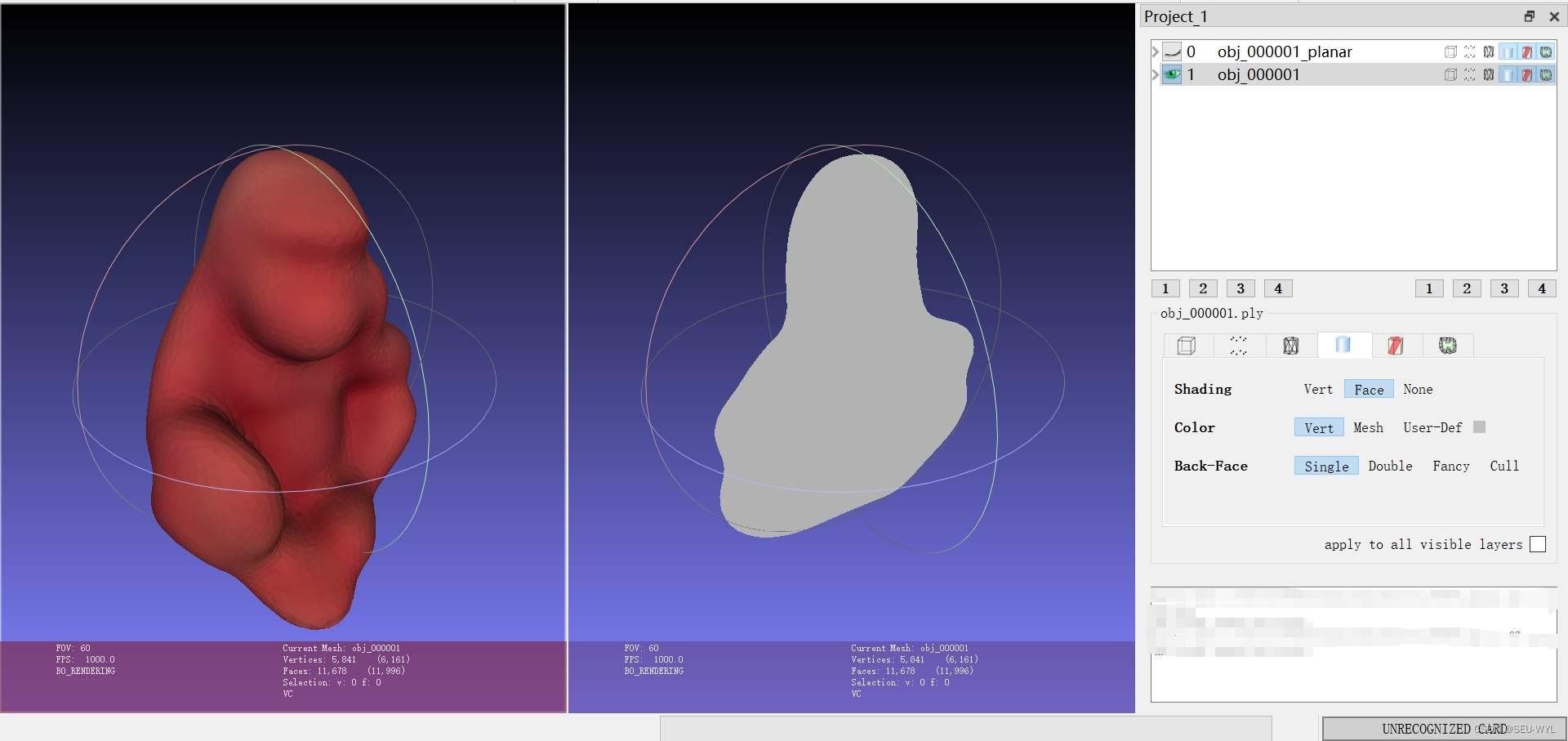
meshlab: pymeshlab保存物体的横截面(compute planar section)
一、关于环境 请参考:pymeshlab遍历文件夹中模型、缩放并导出指定格式-CSDN博客 二、关于代码 本文所给出代码仅为参考,禁止转载和引用,仅供个人学习。 # pymeshlab需要导入,其一般被命名为mlimport pymeshlab as ml# 本案例所使用的3D模型为压缩包中的obj_000001.ply,请将其与本脚本放置在同一文件夹内。input_file
智能电网学习2---Section 4和5
Section 4 Algorithm 1. GREEDY ALGORITHM 这个主要是第一次,当m = 1的时候,是要通过公式(1),求得全局最优的一个MDMS, 而这个时候的xij肯定是所有的Concentrator都连在这第一个MDMS上面来算的,因为要满足约束(2) 但是当选了第一个之后,即m > 1之后,因为xij已经满足(2),所以在步骤4中再计算(1)最小的时候,