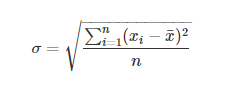今天尝试了一下md的编辑器，不知道有没有什么改变 [NOI1999] 生日蛋糕 题目背景 数据加强版 link 题目描述 7 月 17 日是 Mr.W 的生日，ACM-THU 为此要制作一个体积为 N π N\pi Nπ 的 M M M 层生日蛋糕，每层都是一个圆柱体。 设从下往上数第 i i i（ 1 ≤ i ≤ M 1 \leq i \leq M 1≤i≤M）层蛋糕是半径为

题目链接 点此快速前往 题目总分析 就和我说的一样，这道题就是DFS加剪枝，非常好的一道题 我起初看到这个题我根本不知道怎么dfs才是正确的， 感觉变量有这么多不确定的，每一层的半径，每一层的高度，而且这之间的联系在刚看到这个题的我看来十分的小，应该是我太菜了导致的 深入往下看，你就发现实际上这道题已经告诉了你每一层的限制了，并不是完全无从下手，至少你知道这一层的半径和高度一定小于等于它

居然又是搜索题 本来以为是贪心 后来发现搜索加剪枝 轻松过 剪枝大法好!!!!!!!!!!!!! 注意题目中的 pi是常数 派  我开始以为是单位啥的.. #include <iostream>using namespace std;int n,m;int min_s=1000000000;int SS[25],VV[25];void dfs(int s,int

8.24的生日蛋糕 题面理清题面从零分到达ac的心路历程 思路放一波代码最后的知识小分享 题面 题目背景 7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层 生日蛋糕，每层都是一个圆柱体。 设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求 R i &gt; R i + 1 R_i&gt;R_{i+1} Ri​>Ri

有一个三角形木板,竖直立放，上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每个格子的宽度也都等于d，且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。 让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2），且球的中心还会正对着下一颗将要碰上的钉子。例

题目描述 题解 这道题难就难在这一个均方差公式怎么搞，我们不妨对这一个算式进行化简。 = ∑ ( x i 2 − 2 ∗ x i ∗ x ‾ + n ∗ x ‾ 2 ) n =\sqrt \frac{\sum (x_i^2-2*x_i*\overline x+n*\overline x^2)}{n} =n∑(xi2​−2∗xi​∗x+n∗x2)​ ​ = ∑ x i 2 −