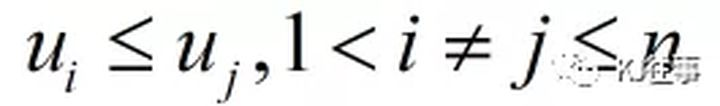mtz专题
TSP with Miller-Tucker-Zemlin (MTZ) model
高级算法课程作业 目录 1. TSP with MTZ模型及解释2. 求解TSP with MTZ3. 实验总结与心得 1. TSP with MTZ模型及解释 模型解释如下: 目标函数z,对应TSP问题哈密顿回路各有向路径的距离之和;约束1的数学含义是任意节点 (城市) i i i 的出度为1,在TSP问题中对应着每个城市只有一个出边;约束2的数学含义是任意节点 (
点击化学 PEG 试剂:1802907-92-1,Mtz-PEG4-NHS,甲基四嗪-四聚乙醇-活性酯
【中文名称】甲基四嗪-四聚乙醇-活性酯 【英文名称】 Methyltetrazine-PEG4-NHS ester,Mtz-PEG4-NHS 【结 构 式】 【CAS号】1802907-92-1 【分子式】C24H31N5O9 【分子量】533.54 【基团部分】Methyltetrazine 【纯度标准】95+% 【包装规格】5g,10g,25g,可以提供核磁图谱及相关质量证明图谱 【是否
规划路径中的子问题——子圈消去的DFJ和MTZ约束
规划路径中的子回路 转自知乎:https://zhuanlan.zhihu.com/p/159270139 TSP问题包含两个重要的约束。约束1:进入点i的次数与从点i出发的次数相等,且次数为1;约束2:消除子回路约束。 对于TSP问题,图1和图2所示路径都满足约束条件1,但只有图1是正确的路径(仅仅有一个回路,TSP问题的特点);而像图2将一个回路拆成了两个及两个以上的回路情况,将每
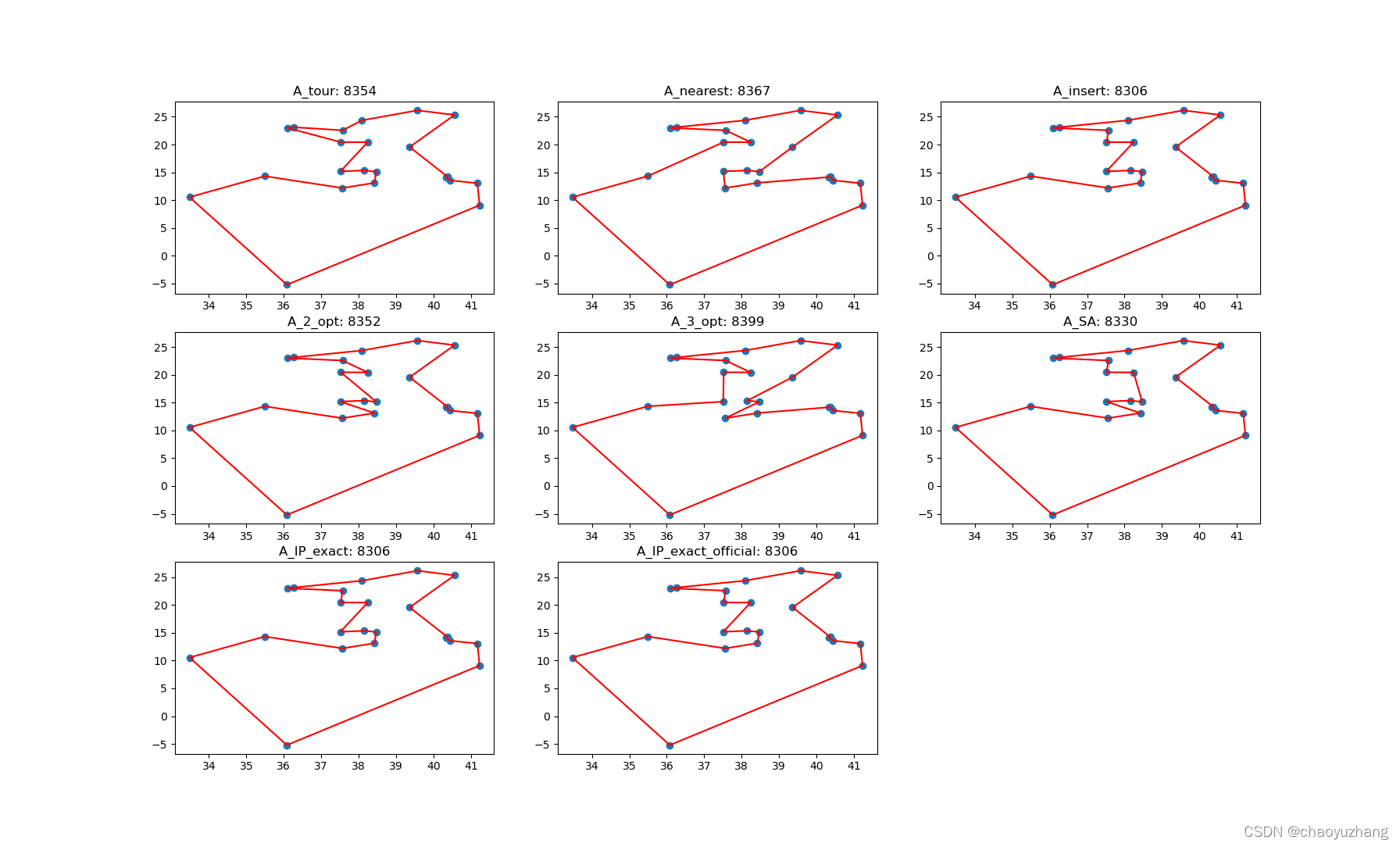
39、TSP的几种精确求解方法(DFJ、MTZ、最短边破圈式、行生成式)和启发式方法(插入法、近邻法、2-opt、3-opt、模拟退火)
0、定义 TSP(Traveling Salesman Problem),旅行商问题,又名旅行推销员问题、货郎担问题 假设一个旅行商要拜访n个城市,每个城市只能经过一次,且最后要回到起点,问如何走路程最短 1、整数模型 设cij为第i个点到第j个点的距离,xij表示是否从走到 1.1、DFJ整数模型 该模型较好理解,前面两个约束保证对每个点入度为1,出度也为1,第三个约束保证每