这是一个解法很简单，但是需要仔细考虑的问题。开始的时候可能会认为是攻击力越高越先处理。但是仔细考虑之后贪心点不仅仅由攻击力决定，还要它的生命值同时决定。勇士在攻击一个怪兽的同时别的怪兽也在攻击勇士，他们的伤害也在叠加。所以优先消灭的怪兽有两个因素同时的决定即有怪兽的攻击力和生命值的比值决定，攻击和生命值比值高的怪兽需要先处理掉。同时要注意此题的结果的取值范围。最终的结果需要使用long long型

好久没写树形DP手生疏了。 题意： 每个点权值为 h p [ x ] + h p [ v ] hp[x]+hp[v] hp[x]+hp[v]，其中 v v v是 x x x的儿子。你可以删掉 m m m个点，求对于 0 ≤ m ≤ n 0≤m≤n 0≤m≤n的每个 m m m能得到的最小权值和。 思路： 定义 d p [ i ] [ j ] [ 0 / 1 ] dp[i][j][0/1] dp

This way 题意： 现在有一棵根为1的树，你要将所有点消除，消除一个点i首先需要消除它的父亲，然后消除i的代价是 也就是hp[i]+还未被消除的所有儿子的hp和 你有一种魔法可以无视所有规则消除掉一个点。 问你这个魔法的使用次数为i(0<=i<=n)次时，最少需要的代价是多少。 题解： 很明显是树形DP，但是枚举儿子的状态转移的话，时间复杂度会变成 n 3 n^3 n3，所以需要

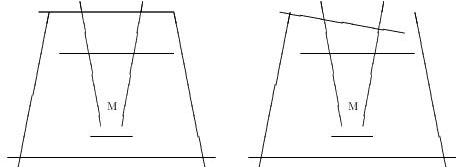
题目链接          本题是2003年ICPC亚洲区域赛会津(日本)赛区的H题 题意         给出一些线段障碍，你的任务是判断怪物能否逃到无穷远处。如下图所示，左图无法逃出，右图的可以逃出。         输入包含多组数据。每组数据第一行为整数n（1≤n≤100），即线段条数。以下n 行每行4 个整数，即一条线段两端的坐标。假定线段的长度均为正，坐标绝对值不超过50。假

哈喽大家好，有几天没给大家更新二手车系列了，主要是一时之间想不到特别好的车型，因为预算的关系，所以我们这个栏目的售价将会卡在4~5万元左右，是国内绝大多数人努力都可以够得着的价格，也是国产中大排的新车售卖的价格区间，超过这个价格范围的我觉得受众面太小，写的意义就不大了，所以这个初衷写在最前面，这个系列会持续更新，但是像之前的一天一更是做不到了，这个预算内的车选择确实不多。1993年第一代Monst

Oh!Monster是由八月印象（北京）科技有限公司新近发布的一款日系风格的2D横版出兵防御游戏，超萌的人设，唯美细腻的画风，加上丰富的剧情和具有挑战性的关卡，使得这款国产新作一登陆iPhone平台就引发了众多关注。这款游戏究竟有哪些亮点和不足，雷锋网小编第一时间进行了上手试玩体验。 作为一款类塔防的即时战略休闲游戏，Oh!Monster在剧情安排和关卡设置上都很见心思，玩家可以选择不同的兵

通过超过10小时的实时专业培训，了解如何从头开始雕刻弗兰肯斯坦的怪物。我们涵盖了基本的面部解剖，雕刻眼睛，耳朵，鼻子和嘴巴，如何给角色漂亮的毛孔，如何雕刻皱纹，以及如何给你的雕塑添加定义。我们在本课程中教授的简单易用的技术将帮助你很快将你的雕塑提升到一个新的水平！FlippedNormals – Sculpting Frankenstein’s Monster 标题:flipped nor