mle专题
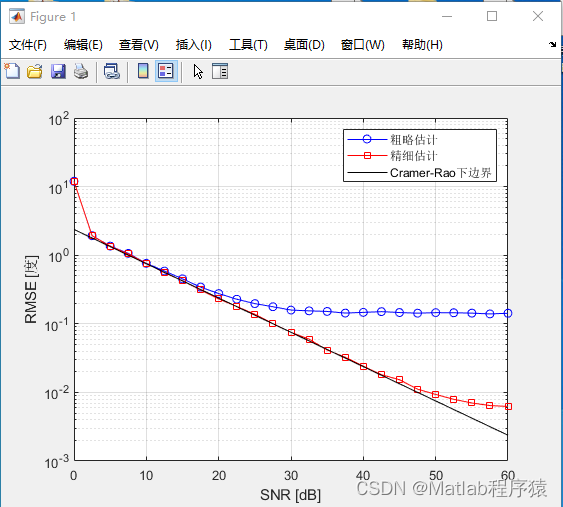
【MATLAB源码-第186期】matlab基于MLE算法的8天线阵列DOA估计仿真,对比粗估计、精确估计输出RMSE对比图。
操作环境: MATLAB 2022a 1、算法描述 第一部分:基本概念与系统设置 方向到达估计(Direction of Arrival, DOA)是信号处理中一项重要的技术,主要用于确定信号的到达方向。这种技术在雷达、无线通信和声纳等领域中有广泛的应用。DOA估计的核心目的是从接收到的信号中提取出信号源的位置信息。 在基于网格搜索的最大似然估计(Maximum Likelihood E
MLE、MAP、贝叶斯估计、MCMC、EM
机器学习中的MLE、MAP、贝叶斯估计 - 李文哲的文章 - 知乎 https://zhuanlan.zhihu.com/p/37215276 上面这篇文章对所提到的三种方法做了清晰的对比。总结图: 另外文中总结:几点重要的Take-aways: 每一个模型定义了一个假设空间,一般假设空间都包含无穷的可行解;MLE不考虑先验(prior),MAP和贝叶斯估计则考虑先验(prior);ML
极大似然估计(MLE)和贝叶斯估计(MAP)
极大似然估计(MLE)和贝叶斯估计(MAP) 标签(空格分隔):机器学习笔记 极大似然估计与贝叶斯估计是统计中两种对模型的参数确定的方法,两种参数估计方法使用不同的思想。 前者来自于频率派,认为参数是固定的,我们要做的事情就是根据已经掌握的数据来估计这个参数(上帝眼中参数 θ \theta早已经固定了,带入 xi x_i样本来求 θ \theta,根据样本来求 θ \theta,最大的
先验概率、后验概率、最大似然估计(MLE)
本文假设大家都知道什么叫条件概率了(P(A|B)表示在B事件发生的情况下,A事件发生的概率)。 先验概率和后验概率 教科书上的解释总是太绕了。其实举个例子大家就明白这两个东西了。 假设我们出门堵车的可能因素有两个(就是假设而已,别当真):车辆太多和交通事故。 堵车的概率就是先验概率 。 那么如果我们出门之前我们听到新闻说今天路上出了个交通事故,那么我们想算一下堵车的概率,这个就叫
【图解例说机器学习】参数估计 (MLE and MAP)
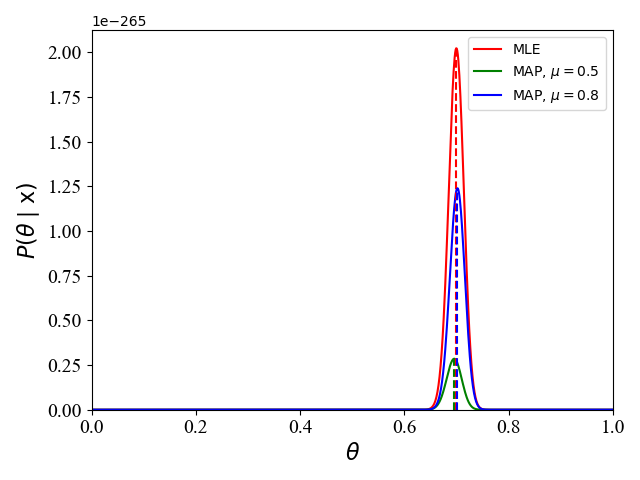
参数估计:给定一个数据集,我们希望用一个给定的分布去拟合该数据集的分布,确定该分布的参数的过程就是参数估计。例如,我们用二项分布去拟合多次投掷硬币的情况,计算该二项分布的最优参数(出现正面的概率 θ \theta θ)就是参数估计。 下面,我们介绍在机器学习中常用的参数估计:极大似然估计 (Maximum Likelihood Estimation, MLE),最大后验概率估计 (Maximu
先验概率、最大释然估计(MLE)与最大后验估计(MAP)
前言 在数据分析和机器学习中,估计是一个很重要的内容,这里着重介绍下极大似然估计与极大后验估计。 最大似然估计(MLE) 最大似然估计是模型已定,参数未定时的一种估计方法。比如说对于抛硬币而言,模型已定,可以看做是多个伯努利实验,我们所不知道的是这个硬币正面朝上的概率 p p,所以我们的任务就是估计pp的值。极大似然估计的思想是,对于已经给定的一些观测数据,参数 p p的取值应使得取
#通俗理解# 从极大似然估计(MLE)到最大期望(EM)算法
文章目录 1. 期望(Expectation)2. 极大似然估计(Maximum Likelihood Estimate,MLE)3. 最大方差估计(Expectation-Maximum,EM)对于第2步的解释对于第3步的解释对于第4步的解释 1. 期望(Expectation) 顾名思义,最大期望算法就是让某个函数的期望最大化从而得到最优参数,首先我们先要了解期望的公式:
最大似然估计法(MLE)
最大似然估计(Maximum Likelihood Estimation),是一种统计方法,它用来求一个样本集的相关概率密度函数的参数。最大似然估计中采样需满足一个很重要的假设,就是所有的采样都是独立同分布的。 一、最大似然估计法的基本思想 最大似然估计法的思想很简单:在已经得到试验结果的情况下,我们应该寻找使这个结果出现的可能性最大的那个 作为真 的估计。
以色列理工暑期学习-MLE、MAP参数估计方法
小编有幸参加到以色列理工的暑期交流项目中,并选择了《机器学习导论》这门经典课程,进行再次学习并回顾知识点查缺补漏; 既然是作为导论,国外的课程和国内的课程的区别在哪里?我觉得很重要的两点是:逻辑性和学习性。 很多在国外交流过的同学,或者看过国外大学视频的同学应该都有一些体会,逻辑性在于课程如何引入很重要;主要是通过一两句简单的概述,让学生明白这门课最基础的内容和最实用的应用,然后逐步递推,从e