leonardo专题
poj 3128 Leonardo's Notebook(置换的幂)
http://poj.org/problem?id=3128 大致题意:输入一串含26个大写字母的字符串,可以把它看做一个置换,判断这个置换是否是某个置换的平方。 思路:详解可参考置换群快速幂运算 研究与探讨。 可以先正着考虑一个置换的平方出现什么情况。对于置换中的循环,若其长度为偶数,平方以后一定分成了两个长度相等的循环,若长度是奇数,平方以后仍是一个循环,长度不变。因此,考虑
LA 3641 Leonardo's Notebook / 置换
给出26个大写字母组成 字符串B问是否存在一个置换A使得A^2 = B 书上的证明结论 2个长度为n的相同循环相乘 n为奇数时结果为1个长度为n的循环 n为偶数时分裂成2个长度为n/2的循环 倒过来 对于一个长度为n为奇数的循环B都能找到一个长度为n的循环A使得A^2 = B 对应任意2个长度为n的不相交循环B,C 都能找到一个长度为2n的循环A 使得A^2 = BC 所以对于B=(1,
POJ3128 Leonardo's Notebook【置换群】
题目链接: http://poj.org/problem?id=3128 题目大意: 给你一行共 26 个字母,代表一个置换。问:这个置换能否为某个置换平方的结果。 解题思路: 这道题可参考《置换群快速幂运算研究与探讨》,里边有详解。这里放上结论。 结论一: 一个长度为 l 的循环 T,l 是 k 的倍数,则 T^k 是 k 个循环的乘积,每个 循环分别是循环 T 中下
UVA - 12103 Leonardo's Notebook
题目:链接 题意:给出26个大写字母的置换B,问是否存在一个置换A,使得A^2 = B 思路:总结一个规律:两个长度为n的相同循环相乘,当n为奇数时结果也是一个长度为n的循环;当n为偶数的时候分裂成两个长度为n/2的循环,所以对于一个长度为n的奇数循环都能找到一个长度为n的循环使得A^2=B,对于两个长度都为n的不相交的循环(不要求是偶数)B和C,都能找到一个长度为2n的循环A,使
uva 12103 - Leonardo's Notebook(置换)
题目链接:uva 12103 - Leonardo's Notebook 题目大意:给出26个字母的置换,问是否存在一个置换A,使得A2=B 解题思路:将给定置换分解成若干个不相干的循环,当循环的长度n为奇数时,可以由两个循环长度为n的循环的乘积得来,也可以由两个循环长度为2n的拆分而来;对于长度n为偶数的,只能由两个循环长度为2n的拆分而来,所以判断是否存在有循环长度为偶数的个数是奇数
UVA 12103 - Leonardo's Notebook(数论置换群)
UVA 12103 - Leonardo's Notebook 题目链接 题意:给定一个字母置换B,求是否存在A使得A^2=B 思路:任意一个长为 L 的置换的k次幂,会把自己分裂成gcd(L,k) 分, 并且每一份的长度都为 L / gcd(l,k),因此平方对于奇数长度不变,偶数则会分裂成两份长度相同的循环,因此如果B中偶数长度的循环个数不为偶数必然不存在A了 代码:
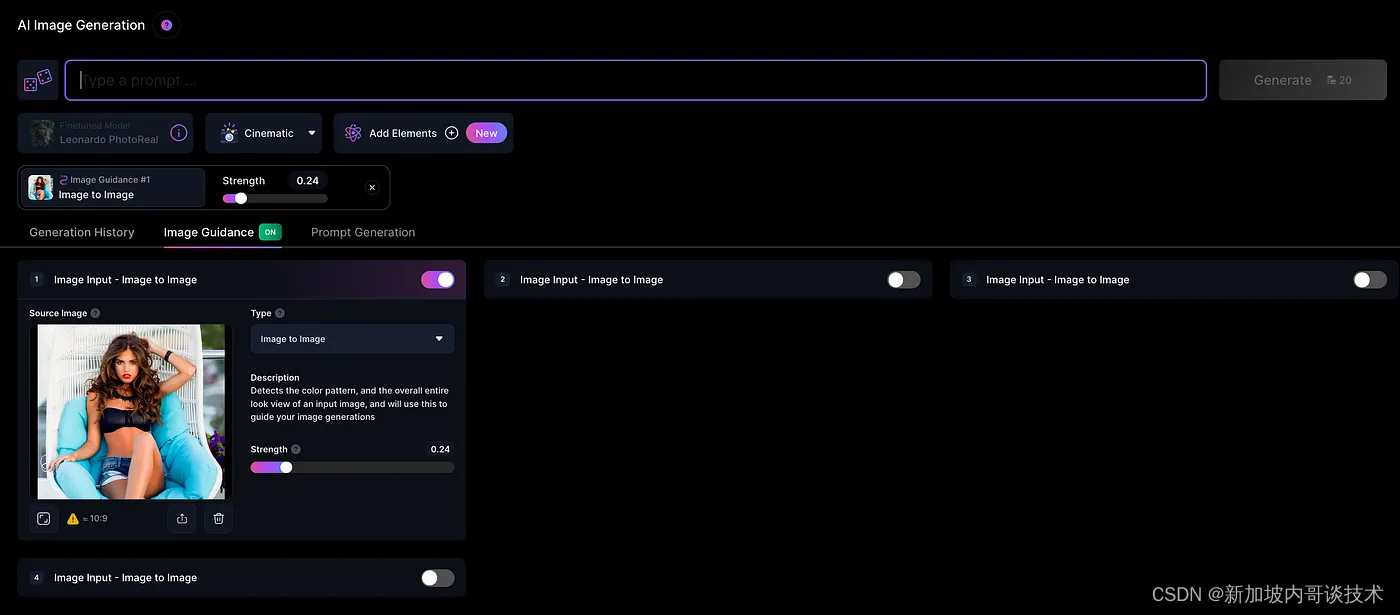
很抱歉,Midjourney,但Leonardo AI的图像指导暂时还无人能及…至少目前是这样
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领域的领跑者。点击订阅,与未来同行! 订阅:https://rengongzhineng.io/ 看看上面的图片,问问自己,三张中哪一张绝对是AI生成的图像。然后考虑,哪一张
SPOJ LEONARDO Leonardo Notebook
Description — I just bought Leonardo’s secret notebook! Rare object collector Stan Ucker was really agitated but his friend, special investigator Sarah Keptic was unimpressed. — How do you know it
AI绘画新秀-免费使用-Leonardo(Midjourney对手)注册教程
本教程收集于:AIGC从入门到精通教程 AI绘画新秀-免费使用-Leonardo(Midjourney对手) 保姆级注册教程 目录 一、写在前面的话。 二、纯文字教程 2.1 Leonardo注册教程: